In the Last edition we learnt how a Neuron works..
Here we will learn about Hardware Design of Neuron
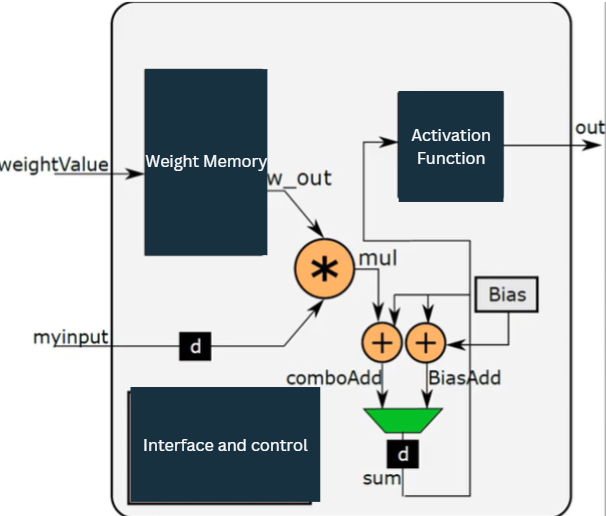
The Weight Memory
reg [dataWidth-1:0] mem [numWeight-1:0];
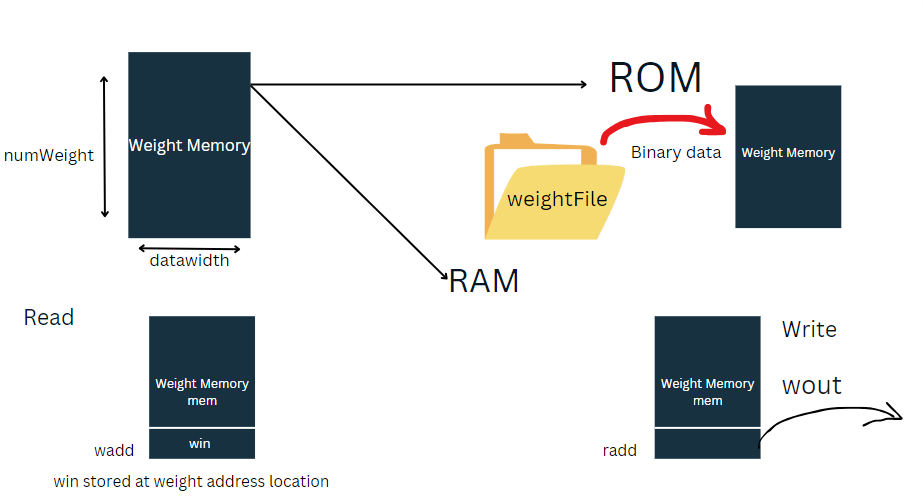
That is why our weight memory code will be as such
`ifdef pretrained
initial
begin
$readmemb(weightFile, mem);
end
`else
always @(posedge clk)
begin
if (wen)
begin
mem[wadd] <= win;
end
end
`endif
always @(posedge clk)
begin
if (ren)
begin
wout <= mem[radd];
end
end Let us learn how the weights are loaded into neuron, provided that neuron is not pretrained
We will weight value from all 1s, So that when valid weight and correct layer and configuration of neuron is identified, Wddr will be incremented with this value will be stored from 0 address..
always @(posedge clk)
begin
if(rst)
begin
w_addr <= {addressWidth{1'b1}};
wen <=0;
end
else if(weightValid & (config_layer_num==layerNo) & (config_neuron_num==neuronNo))
begin
w_in <= weightValue;
w_addr <= w_addr + 1;
wen <= 1;
end
else
wen <= 0;
end
Now , we will multiply myinput with wout
always @(posedge clk)
begin
mul <= $signed(myinputd) * $signed(w_out);
endWhy did we added delay to input
Whenever the input comes, it should be multiplied with corresponding weight.
Our weight memory works sequentially,it needs one clock latency so input also needs some delay..
Now , we will add product of weight memory and input and add it with previous sum.
assign comboAdd = mul + sum
So, now with this 2 possibilities arise i.e overflow and underflow..
If the msb of multiply output and sum is 0 and combo add is 1 than it is overflow
than we will add 0 to msb of sum and rest bit will be made 0.
Similarly the case for underflow is made…
But above dont work for last multiplication, because for last multiply we need to add bias to multiply output
assign BiasAdd = bias + sum
always @(posedge clk)
begin
if(rst|outvalid)
sum <= 0;
else if((r_addr == numWeight) & muxValid_f)
begin
if(!bias[2*dataWidth-1] &!sum[2*dataWidth-1] & BiasAdd[2*dataWidth-1]) //If bias and sum are positive and after adding bias to sum, if sign bit becomes 1, saturate
begin
sum[2*dataWidth-1] <= 1'b0;
sum[2*dataWidth-2:0] <= {2*dataWidth-1{1'b1}};
end
else if(bias[2*dataWidth-1] & sum[2*dataWidth-1] & !BiasAdd[2*dataWidth-1]) //If bias and sum are negative and after addition if sign bit is 0, saturate
begin
sum[2*dataWidth-1] <= 1'b1;
sum[2*dataWidth-2:0] <= {2*dataWidth-1{1'b0}};
end
else
sum <= BiasAdd;
endThis sum now goes to activation function
Activation function supports 2 functions,one is RELU and other is sigmoid
generate
if(actType == "sigmoid")
begin:siginst
//Instantiation of ROM for sigmoid
Sig_ROM #(.inWidth(sigmoidSize),.dataWidth(dataWidth)) s1(
.clk(clk),
.x(sum[2*dataWidth-1-:sigmoidSize]), //send the sum value
.out(out)
);
end
else
begin:ReLUinst
ReLU #(.dataWidth(dataWidth),.weightIntWidth(weightIntWidth)) s1 (
.clk(clk),
.x(sum),
.out(out)
);
end
endgenerateIn next editions we will learn, even more deeper this was a overview of implementation of Neuron!
Stay tuned
legal steroids for skinny guys
References:
https://travelersqa.com/user/ariesclover0
buy real steroids
References:
https://md.entropia.de/MeU55Yj0S3OtLghaEiEv9g/
Эта процедура помогает очистить кожу и улучшить её состояние.
На epilstudio.ru разобрали фото до и после процедуры.
Советую прочитать тем, кто интересуется уходом за кожей.
Also visit my webpage салициловая кислота
what happens if i side with the institute
References:
https://www.divephotoguide.com/user/townbath1
n9dtnn
Многие интересуются, какой способ удаления лучше выбрать.
На laser-wart-removal-in-moscow.ru подробно рассказали
о методах удаления папиллом.
Советую прочитать тем, кто задумывается
об удалении новообразований.
My web-site :: лечение кожи
what is the best steroid
References:
https://www.bidbarg.com/legal/user/crylaura0
In Figure 2A, the cardiac operate parameters extracted from the RT short-axis cine analysis are depicted, tracing the development from rest to 3 phases of exercise for every volunteer. Plyo jacks are sluggish jumping jacks. If the impression is a lot, do the move with out jumping. 4. Land with tender joints, lower into a lunge, and repeat, jumping and switching sides. 2. Lower right into a squat and jump forward in an explosive motion. 2. Squat as little as you’ll be able to, taking your torso barely forward with out rounding the again. 3. Jump to the left, again taking a wide step, and land in your left foot. Modify this cardio exercise by elevating your upper body, taking a few of the burden off your arms, and putting it in your decrease body, which is stronger. This is a complicated, excessive-affect cardio exercise, so protect your joints by touchdown with tender knees. When you need to change, attempt a staggered landing (one foot lands a bit earlier than the opposite one). One anchor is preserved at Point Pleasant Park in Halifax because the Bonaventure Anchor Memorial. Start at this time by incorporating one or two of those exercises into your routine and progressively build from there. There are specific stretching workout routines that can be accomplished to correct and maintain our full vary of movement of all the muscle groups.
Feel free to surf to my web blog; http://8.138.149.79:3000/rebeccafender5
how much does dianabol cost
References:
Cops on steroids (https://cuttify.io/ermahenninger)
If there’s a most necessary organ, it’s the mind. The brain solves issues, shops and retrieves recollections, directs your physique to breathe, blink, and digest food, and much more. Protecting your brain with overall good well being can pay off by promoting coronary heart well being, too. Research reveals that controlling danger elements linked to coronary heart illness, including obesity, high blood stress, and diabetes, helps preserve brain operate. Regular exercise also promotes brain “fitness.” Physically active adults are much less likely to experience age-related declines in considering, learning, and judgment abilities, in keeping with the 2018 Physical Activity Guidelines for Americans. Most healthy people need at the very least a hundred and fifty minutes per week of moderate-depth activity, equivalent to brisk walking. A balanced food regimen with the right variety of calories helps reduce the risk for the situations that can hurt the mind. Antioxidants: Vitamin C is a robust antioxidant that helps protect mind cells by reducing free radical harm-harmful types of oxygen formed in the physique.
My page https://www.03shuo.com/home.php?mod=space&uid=142323&do=profile&from=space
If you ask health care providers about the most challenging condition to treat, chronic pain is mentioned frequently. By its nature, chronic pain is a complex and multidimensional experience. Pain perception is affected by our unique biology, our mood, our social environment, and past experiences. If you or a loved one is suffering from chronic pain, you already know the heavy burden. Given the ongoing challenges of chronic pain management coupled with the consequences of the opioid epidemic, pain management practitioners and their patients are searching for effective and safer alternatives to opioids to alleviate pain. With the legalization of marijuana in many states and resulting cultural acceptance of this drug for recreational and medical use, there has been an increased interest in using cannabis for a myriad of medical problems, including pain. Cannabis (most commonly obtained from the Cannabis indica and Cannabis sativa plants) has three major components: cannabinoids, terpenoids, and flavonoids. While there are over a hundred different cannabinoids, the two major components are tetrahydrocannabional (THC) and cannabidiol (https://morphomics.science/wiki/User:RicoFruehauf).
best way to inject steroids
References:
steroids to build muscle, https://git.galaxylabs.ca/sebastiankinse,
is clear muscle a steroid
References:
legal supplements similar to steroids (http://git.baobaot.com/angelinar93493)
aas bodybuilding
References:
best online steroids (https://gitea.alaindee.net/hyebaptiste402)
before after steroids pictures
References:
http://rhx0.top:3000/benniemaurice6
what is the safest anabolic steroid
References:
http://gitlab.dev.jtyjy.com/gusgoheen35413
what are legal
References:
best supplement stack for muscle gain (https://sithcom.de/amadoshirk668)
From there, anywhere from 250 to 500 blisters will unfold across the average unvaccinated person and should appear within the eyelids, mouth and genitals. The extreme complications pose a better menace to certain teams of people, which we’ll discuss in the next part. Mouse over the chicken pox complications to see how they have an effect on the body. In the following part, we’ll discuss these complications and who needs to be concerned. They’ve found McQueen. With mixed feelings, he says goodbye to Sally, who thanks him for bringing the town back to life. Suddenly, police helicopters and Tv information digicam crews swarm the city. McQueen fortunately spends the whole day giving new business to everyone in city — he gets new tires, organic gas, a paint job, and even a touristy bumper sticker. Everyone in town celebrates by cruising the principle avenue. This basic substance, known as “https://rentry.co/30606-exploring-gluco-extend-your-ultimate-guide-to-glucose-support,” is your body’s fundamental source of vitality. If it stays there, your body places out more hormones, together with one known as cortisol, also called “the stress hormone,” partially as a result of it helps control issues like your mood and concern. These seafood choices are also wealthy in copper, a mineral that helps the physique absorb iron and produce hemoglobin.
Сильное воспаление кожи может приводить к рубцам
и осложнениям.
На kpacota.top нашла информацию о современных методах
лечения.
Информация будет полезна подросткам и взрослым.
Visit my web blog: сайт kpacota.top
Wonderful site. Plenty of useful information here.
I’m sending it to a few buddies ans additionally sharing in delicious.
And certainly, thanks on your effort!
I could not refrain from commenting. Very well written!
reddit legal steroids
References:
top supplement stacks (https://pinshape.com/users/8748744-sheetday0)
Hi there, I desire to subscribe for this website to take hottest
updates, therefore where can i do it please help
out.
Hi there, I check your blog daily. Your story-telling style is witty, keep doing
what you’re doing!
ipamorelin wirkung
References:
how long does it take For ipamorelin to work (https://www.refermee.com/companies/buy-sermorelin-ipamorelin-10mg-online/)
These are genuinely enormous ideas in concerning blogging.
You have touched some nice things here. Any way keep up wrinting. http://Athrconsultancy.in/employer/euro-girls-escort
ipamorelin to get skinnny
References:
https://www.haphong.edu.vn/profile/filtenborgiiltruelsen89842/profile
ipamorelin long-term side effects
References:
https://healedonly.com/@sherylmireles4
is cjc 1295 ipamorelin a steroid
References:
ipamorelin interacciones – http://osbzr.com/bea28l69690865,
what are the benefits of combining cjc-1295 and ipamorelin
References:
http://www.grainfather.eu/employer/cjc-1295-dosage-calculator-and-chart-a-z-guide
ipamorelin nasal spray for sale
References:
https://cvcentrum.eu/companies/tesamorelin-vs-ipamorelin-key-differences-benefits-and-uses/
after injecting cjc 1295 ipamorelin my body gets hot
References:
ipamorelin Einnahme (https://n28.it/elishaphelan6)
Howdy!This is my first ccomment here so I just wanted
to give a quick shout out aand say I genuinely enjoy reading yoour
articles. Can you suggest any other blogs/websites/forums that cover
the same topics? Appreciate it! https://Penzu.com/public/8228a2acbfbcc129
It’s going to be finish of mine day, buut before end I am reading this impressive
article to increase my know-how. https://justpaste.it/azurslottrustedcasino
certainly like your web-site however you have to text the spelling on several off your posts.
A number of them are rife with spelling issues aand I inn finding iit very bothersome tto tell the truth then again I will certainly comme again again. https://zenwriting.net/c9iadqodtw
Attractive comjponent to content. I just stumbled upon your
website and in accession capital to say that I acquire actually enjoyed account your weblog
posts.Any way I will be subscribing to your feeds and even I
achievement you get entry to consistently fast. https://Marketingstrategies16.wordpress.com
Right here is the right webpage for everyone who hopes to find
out about this topic. You know a whole lot its almost hard to
argue with you (not that I actually would want to…HaHa).
You definitely put a brand new spin on a
subject which has been discussed for decades. Great stuff, just wonderful!
Hi! I know tthis is kind of off-topic however I had too ask.
Does building a well-established blog like yours require a
loot of work? I am completely new to writing a blog but I do write in my journal daily.
I’d like to start a blog so I will be aable to share mmy own experience andd feelings online.
Please let me knw if you have any ideas or tkps forr brand new aspiring bloggers.
Thankyou! https://Glassi-Greyhounds.Mystrikingly.com/
steroid use symptoms
References:
best test for cutting cycle (https://music.michaelmknight.com/frederickrome)
Right away I am ready to do my breakfast, after having my breakfast coming again to read more news.
It’s difficult to find educated people on this subject, however, you seem
like you know what you’re talking about! Thanks
sytropin hgh reviews
References:
sytropin hgh ingredients, https://litvids.org/pasqualepark99,
winstrol and dianabol cycle
References:
https://images.google.co.il/url?q=https://www.valley.md/dianabol-cycle-benefits-and-risks
oral dianabol cycle
References:
what to take after dianabol cycle – https://www.metooo.io/u/6897127c9bfd9664e3f32ded,
The dosage of Anavar relies upon entirely on variables similar to intercourse, age, experience, goal, and different exposures to Anabolics. Anavar (or Oxandrolone) is an Anabolic Androgenic Steroid first introduced into the medical world in 1964. It was originally given to sufferers affected by muscle-wasting illnesses similar to HIV/AIDS. Anavar dosage is something that a lot of people are interested in. Aqueous extract of valerian root (Valeriana officinalis L.) improves sleep quality in man. Effects of oxandrolone on plasma lipoproteins and the intravenous fat tolerance in man. (6) Schroeder, E. T., Zheng, L., Ong, M. D., Martinez, C., Flores, C., Stewart, Y., Azen, C., & Sattler, F. R.
You additionally need to take into consideration your individual personal tolerance to the drug. If you discover that you’re tolerating it well, you possibly can enhance the dosage gradually. As Anavar can be utilized both for bulking and slicing, we will discuss both.
At Asana, we offer efficient, insurance-covered remedy for habit and psychological well being, guided by consultants who understand because they’ve been there. Liver injury signs include jaundice, darkish urine, fatigue, nausea, and stomach pain. Elevated liver enzymes, cholestatic syndrome, and severe problems like peliosis hepatis https://www.valley.md/anavar-dosage-for-men liver tumors may happen. For example, stacking Anavar with Testosterone might help counterbalance check suppression while enhancing muscle-building outcomes.
Before taking any of these, ensure you are in good well being – particularly psychological well being. Anavar could be dosed at around 20 – 40mg per day, while Winstrol may be dosed at 20 – 60mg per day. Personal numbers will depend upon sex, age, experience, objective, and different exposures to Anabolics. Utilizing Anavar with Winstrol is not often suggested as both orals will trigger pressure on the liver and kidneys. Each Anavar and Winstrol are Dihydrogentesttosterone derivatives, that means they won’t trigger an increase in estrogen ranges. This is as a end result of it could cause barely more opposed effects and lower Progesterone.
Submit cycle therapy (PCT) is beneficial after taking Anavar to assist restore your natural testosterone production and forestall any opposed results. It is important to consult with a healthcare skilled to determine the suitable PCT for you. When taking Anavar, the beneficial dosage for men is between mg per day.
Anvarol works by serving to your physique to produce extra phosphocreatine. Phosphocreatine is important for producing energy during brief, intense bursts of exercise, similar to lifting weights. Anvarol might help you to train harder and longer than earlier than, resulting in amplified muscle growth and faster gains in energy and size.
If you’re stacking Anavar with other steroids, it is essential to start with a decrease dosage of Anavar and increase it gradually. Anavar – also identified as Oxandrolone – is a very popular anabolic steroid. Anavar, a well-liked anabolic steroid, is available in varied manufacturers with differing price factors. If you’re seeking to discover the best brand of this steroid while contemplating affordability, this table provides a comprehensive pricing comparison. We’ve included real manufacturers like Alpha Pharma to provide you an idea of the price variations. Take a take a glance at the table below to make an knowledgeable choice when purchasing Oxandrolone.
In addition to its anabolic results, Anavar has a modest impact on metabolic exercise. It can improve basal metabolic price (BMR), which refers to the number of energy burned at rest. This elevation in BMR can contribute to fat loss by utilizing saved body fats as an energy supply. Although most customers have a tendency to make use of it as a compound for the maintenance of muscle mass during a hypocaloric fat loss cycle, its use in reality extends far beyond that. As A Outcome Of of Anavar’s strength being that of 3 times Testosterone, it is very properly potential for Anavar to be successfully utilized as a mass gaining (or even a bulking) agent.
Bedankt voor zulke nuttige content over plinko casino en kansspelen.
http://worldlimobiz.com/R1stClasslimo/2025/04/08/plinko-spel-in-nederland-online-sasino-spel-2/
Excellent goods from you, man. I have understand your stuff previous to and you’re just too fantastic.
I really like what you have acquired here, really like
what you are stating and the way in which you say it.
You make it entertaining and you still care for to keep it sensible.
I can’t wait to read much more from you. This is really a tremendous site.
Процедура улучшает цвет, текстуру и упругость кожи.
На epilstudio.ru разобрали, как проходит процедура.
Советую прочитать всем, кто заботится о красоте кожи.
Подошвенные натоптыши вызывают дискомфорт и боль при ходьбе.
На epilstudio.ru разобрали, как предотвратить их появление.
Советую прочитать всем, кто сталкивался с этой проблемой.
Ортопедические стельки поддерживают
правильное положение стопы и предотвращают деформации.
На epilstudio.ru разобрали, кому особенно рекомендованы стельки.
Советую прочитать всем, кто заботится о здоровье стоп.
Метод подходит для эстетических и медицинских целей.
На epilstudio.ru нашла полезную информацию
о процессе.
Советую прочитать всем, кто ищет современный и безопасный способ удаления новообразований.
Процедура проходит быстро и безболезненно.
На epilstudio.ru разобрали, кому подходит лазерная терапия.
Советую прочитать всем, кто планирует удалять бородавки.
Медицинский педикюр помогает не только улучшить внешний
вид стоп, но и решить проблемы со здоровьем.
На epilstudio.ru нашла полезные рекомендации по уходу
за ногами.
Информация пригодится каждому.
Процедура безопасна и практически безболезненна.
На epilstudio.ru подробно рассказали о преимуществах лазерного метода.
Советую прочитать всем, кто планирует удалять бородавки.
We provide certified translation services to thousands of happy customers since
2011. https://www.footballzaa.com/out.php?url=https://aqueduct-translations.org/inside-translation/how-accurate-is-ai-in-technical-translation-for-regulated-industries/
how much iu of hgh should i take a day
References:
Gesicht Hgh Vorher Nachher (https://sciencewiki.science/wiki/Wachstumshormone_Bodybuilding)
Сервисный центр РемТочка предлагает услуги по диагностике, ремонту и обслуживанию компьютерной техники. Мы специализируемся на решении любых проблем с вашим компьютером, от простых настроек до сложных технических работ. Наши опытные специалисты всегда готовы помочь вам с любыми вопросами, такими как
https://116pc.ru/ связанными с компьютерами и программным обеспечением.
References:
dianabol and winstrol cycle https://www.valley.md/dianabol-cycle-benefits-and-risks
what is considered a high roller at a casino
References:
high roller vegas what is a blackout [http://mcforces.ru/user/racingblouse33/]
References:
anabolic steroids substitutes (https://neurotrauma.world/tb-500-peptide-injections-benefits-dosage-and-risks)
облучатель ультрафиолетовый ультрамиг 311р расческа
how to get big quick without steroids
References:
https://thesecurityexchange.com/employer/kaufen-hgh-deutschland-hgh-online-zu-verkaufen/
Eine einmalige Überdosierung kann zu akuten Nebenwirkungen wie Zittern, Schweißausbrüchen, Starvation, Schwäche, schnellem Herzschlag und Übelkeit führen. Rufen Sie in solchen Fällen sofort Ihren Arzt oder andere Gesundheitsdienstleister an. Die empfohlene Dosis der HGH-Therapie bei HIV-assoziierter Kachexie beträgt zero,1 mg / kgBW oder bis zu 6 mg.
Möglich ist auch die Anwendung einer Progesteroncreme, welche verschiedene Hormone miteinander kombiniert. Die Ernährung, die ein Sort in den ersten fünf Lebensjahren erhält, ist wichtig für sein Wachstum und seine Entwicklung. Tierische Lebensmittel wie Fleisch, Fisch, Eier oder Milchprodukte liefern entscheidende Nährstoffe. Darüber hinaus kann es natürlich auch machen L-Arginin zu supplemetiere. Diese Aminosäure fördert die Durchblutung und unterstützt die Herstellung von HGH im Körper. Schlaf ist wie oben schon erwähnt einer der wichtigsten Faktoren wenn es um die Bildung von HGH geht. Schlafmangel auf der anderen Seite senkt unsere Testosteron und HGH Produktion signifikant.
Symptome wie andauernde körperliche und kognitive Müdigkeit oder dauerhaft fehlende Lust auf Sex können jedoch Indikatoren sein, die auf einen möglichen Mangel hindeuten. Letztendliche Sicherheit kann dir jedoch nur ein Besuch beim Arzt verschaffen. Dieser fertigt auf deinen Wunsch hin ein vollständiges Blutbild an, aus dem hervorgeht, wie es um dein HGH bestellt ist.
Human Progress Hormone (hGH) ist ein in der Hirnanhangsdrüse produziertes Hormon, das wesentlich für die Zellentwicklung und das Wachstum des Körpers verantwortlich ist. Im Bereich der Sportmedizin wird das Potenzial von Wachstumshormon zur Leistungssteigerung und zur Beschleunigung der Regeneration nach Verletzungen untersucht. Obwohl die Anwendung von Wachstumshormon im Sport streng reguliert ist, könnten zukünftige Erkenntnisse zu neuen, legalen Einsatzmöglichkeiten führen, die unter ärztlicher Aufsicht erfolgen. Diese Erkrankung kann auch neurologische Probleme verursachen, einschließlich Gelenkschmerzen, Kopfschmerzen und Karpaltunnelsyndrom. Schlafapnoe ist eine weitere häufige Komplikation, verursacht durch Veränderungen im Kiefer und im Gewebe des Rachens. Diese Risiken verdeutlichen, wie wichtig eine sorgfältige Überwachung und Kontrolle der hGH-Anwendung ist.
Verbesserter Schlaf hat mehr angeborene Vorteile als Sie sich vorstellen. Wenn Sie exogenes HGH injizieren, erhöht es automatisch die Sekretion von Insulin Like Development Factor-1, einem extrem anabolen Hormon. Während das menschliche Wachstumshormon selbst kein dramatisches Muskelwachstum fördert, ist die Kombination mit IGF-1 sowohl für Sportler als auch für Bodybuilder von Vorteil. Mögliche Nebenwirkungen von Wachstumshormon sind Karpaltunnelsyndrom, Hyperglykämie, Schilddrüsenunterfunktion, Flüssigkeitsansammlung und erhöhter Blutdruck. Wachstumshormon hat anabole Wirkungen, die zu Muskelaufbau, Fettabbau und Knochenwachstum führen. Es hat auch optimistic Auswirkungen auf die Regeneration und Heilung von Gewebe. Es ist wichtig zu beachten, dass HGH zum Verkauf keine magische Lösung ist und in Verbindung mit einem richtigen Diät- und Trainingsprogramm verwendet werden sollte.
Vor dem GHRH-Arginin-Test muss der Patient mindestens 8 Stunden nüchtern sein und eine Stunde Ruhezeit einhalten. Dies stellt sicher, dass die Testergebnisse nicht durch äußere Faktoren verfälscht werden. Der Insulin-Hypoglykämie-Test gilt als Goldstandard zur Diagnose eines hGH-Mangels, da er die Hypophyse direkt stimuliert.
Das Wachstumshormon HGH ist unter anderem in Tomaten, Bananen und auch in Mandeln enthalten, und kann der Produktion von Wachstumshormonen, dienlich sein. Damit der Botenstoff möglichst viel Fett den Kampf ansagt, sollte abends keine Kost mit Eiweiß zu sich genommen werden. Außer der Einnahme von wachstumsfördernden Mitteln, gibt es unterschiedliche Möglichkeiten das Hormon auf natürliche Weise zu beeinflussen. Dazu gehört in erster Linie ein gesunder und ausreichender Schlaf, sportliche Aktivitäten (regelmäßiges Training) und nicht zuletzt Unterzucker- Zustände.
Nichtsdestotrotz bleibt der Wachstumshormonspiegel nicht über die gesamte Lebenszeit hinweg gleich, denn insbesondere im Rahmen der Pubertät erreicht die Hormonkonzentration im Blut bei beiden Geschlechtern einen kräftigen Peak. Dieser Peak hält in der Regel bis in die frühen Zwanziger, bis die Konzentration dann auf ein moderates Niveau heruntergefahren wird. Wie schon oben erwähnt, vermindert das Wachstumshormon das Körperfett und wirkt stark anabol, d.h. Ich halte es daher für ein Hormon, das prädestiniert ist, bei Männern eingesetzt zu werden (wenn es eine medizinische Indikation dafür gibt).
Gonadotropine wirken auf die Keimdrüsen und übernehmen im Körper somit eine Übermittlerrolle. HCG wird während der Schwangerschaft, besonders zu Beginn, in hohen Mengen produziert und in die Blutbahn abgegeben. Es steuert die Ausschüttung des Hormons Progesteron, das während der Schwangerschaft die Reifung weiterer Eizellen verhindert und für die Entwicklung der Milchdrüsen wichtig ist. Wir haben zwar bereits erwähnt, dass unser Körper Wachstumshormone wie das HGH sowohl zum Muskelaufbau, als auch für die Regeneration des gesamten Organismus benötigt. Dennoch stellt sich mit Recht die Frage danach, warum wir dieses Wachstumshormon, das dem Namen nach vor allem in der Section unseres Längenwachstums eine tragende Rolle spielt, auch im Alter noch brauchen? Die Antwort ist einfach, denn dieses Hormon hat ebenfalls zahlreiche Eigenschaften und Aufgaben, die nicht im wörtlichen Sinne mit seinem zugegebenermaßen etwas unglücklich gewählten Namen in Verbindung gebracht werden können. Dazu zählt beispielsweise die Aufrechterhaltung des Sexualtriebes, der Verhinderung degenerativer Veränderungen im Organismus sowie Aufrechterhaltung der geistigen Leistungsfähigkeit.
Wachstumshormon (Somatropin oder auch human Growth Hormone, hGH genannt) ist ein Hormon, das von der Hirnanhangdrüse (Hypophyse) ausgeschüttet wird.
References:
https://razib.cretechbd.com/employer/wachstumshormone-kaufen-hgh-authorized-on-line-ohne-rezept-in-deutschland-bestellen/
Es ist auch wichtig zu beachten, dass HGH einen synergistischen Effekt mit anderen Substanzen haben kann. Eine der Hauptfunktionen von Human Growth Hormone im Körper ist die Stimulierung und Beschleunigung des Wachstums und der Teilung von Zellen und Geweben. Wenn Sie eine androgene Substanz mit bestimmten Nebenwirkungen, einschließlich des HGH, einnehmen, wird sichergestellt, dass diese Prozesse mit einer höheren Geschwindigkeit stattfinden. Aus diesem Grund ist es wichtig zu beachten, dass HGH das Wachstum der mit Gyno verbundenen Fettgewebe beschleunigt, wenn Sie Angst vor Gynäkomastie haben. Abgesehen von diesen häufigen Anliegen gibt es auch sehr häufige Symptome, die auftreten können, wenn Sie sich für die Anwendung von HGH entscheiden.
Das Whey Protein liefert einem Körper besonders hochwertiges Eiweiß und ist in der Wirkung für jeden ambitionierten Kraftsportler, eine ideale Ergänzung zur normalen Ernährung. Aber nicht nur Sportler interessieren sich dafür, sondern auch die Forschung(9). Whey kommt aus dem englischen und steht übersetzt für Molke, die als Nebenprodukt bei Milchverarbeitung entsteht. In erster Linie hinterlässt das Complement HGH X2 seine positiven Wirkungen im Wachstumsfaktor bei Leber, Knochen und auf Zellen vom Fettgewebe. HGH steigert weiterhin den Blutzuckerspiegel, kurbelt den Aufbau von Eiweiß an und kann perfekt in die normale Nahrung integriert werden.
Bis zu zehn Tagen gilt Ibuprofen für die meisten Menschen jedoch als sicher. Haben Sie starke Schmerzen, die länger als ein paar Tage anhalten, sollten Sie dies trotzdem von einem Arzt oder einer Ärztin abklären lassen. Vor allem Menschen mit Herz-, Leber- oder Nierenproblemen sowie Asthmatiker sollten daher vor der regelmäßigen Einnahme von Ibuprofen mit Ihrem Arzt oder Ihrer Ärztin sprechen. Denn Ibuprofen hat Wechselwirkungen mit zahlreichen anderen Arzneistoffen. Beispielsweise schwächt Ibuprofen die Wirkung von blutdrucksenkenden Medikamenten und kann auch mit Arzneien zur Behandlung eines Typ-2-Diabetes reagieren.
Herstellung einschränkt, jedoch gut mit einer Ersatztherapie in Type von Gel, Pflaster oder Injektionen und unter Einbeziehung von Sport, behandelbar ist. Durchaus wichtig beim Bedarf, um Muskelmasse zu steigern, sind bei der Nahrungsaufnahme pro Tag zwei Makronährstoffe, die sich aus dem richtigen Eiweiß und aus Kohlenhydraten zusammensetzen. Neben Proteinpräparaten benötigen Sportler für optimales Muskelwachstum zusätzliche Supplemente wie Kreatin für Kraftsteigerung, BCAAs für Regeneration und Beta-Alanin für verbesserte Ausdauer. Mit Krafttraining allein ist es nicht getan, denn mangelt es dem Körper an wichtigen Makro-, als auch an Mikronährstoffen, fehlen den Muskeln wichtige Wirkstoffe für ein perfektes Wachstum, um wirklichen Trainingserfolg zu sehen. Die Gründe ein Muskelwachstum voranzutreiben, sind von Mann zu Mann unterschiedlich.
Diejenigen, die dieses Hormon regelmäßig einnehmen, können eine wiederholte Belastung im Handgelenksbereich spüren. Dies ist eine weitere Nebenwirkung des menschlichen Wachstumshormons, da eine erhöhte Muskelmasse den Karpaltunnel übermäßig belastet . Wenn die Dosierung gesenkt wird, verschwinden die vorübergehenden Nebenwirkungen.
Die meiste HGH-Ausschüttung passiert im Tiefschlaf – besonders in der ersten Nachthälfte. Eine in einer 1994 erschienenen Ausgabe von “Annual Review of Drugs” veröffentlichte Studie verwies auf klinische Studien mit HGH-Therapie das geschah bei Erwachsenen. Die Ergebnisse dieser Studien zeigten dass HGH-Konsumenten von einer erhöhten Muskelmasse einer verringerten Fettmenge und einer allgemeinen Verbesserung ihrer Lebensqualität berichteten. Die Studie schloss mit der Feststellung dass medizinische Internisten möglicherweise entscheiden müssen ob HGH eine geeignete Behandlung ist um “Aspekte des normalen Alterungsprozesses zu reparieren”. HGH senkte den Nicht-HDL-Cholesterinspiegel in allen Gruppen, wobei der Rückgang zwischen 6,6 und 8,four % lag.
Die oben zitierte Studie zeigte nicht diese Nebenwirkung, sodass ich die Ergebnisse der Überdosierung persönlich für zu weit hergeholt ansehe. Andere wiederum stellten eine kurze und leichte Änderung im Herzschlag, sowie in der Atmung fest. Da ich zu den letztgenannten Effekten keine Studien vorzuweisen habe, schließe ich diese Wirkungen einzig und allein auf die indirekte Stimulation der Wachstumshormone zurück. Wobei sicher das vermehrte HGH diese Wirkungen in sehr sehr geringem Maße verursacht haben wird. In dieser Studie wurden 19 Probanden untersucht, die GABA einnahmen und mit einer Placebogruppe bestehend aus 18 Probanden vergleichen. Dies bewirkte einen Anstieg um 500% im Vergleich zur Placebogruppe und zum Ausgangsniveau.
Um die Wirksamkeit von GABA zu erhöhen, wird empfohlen es zwischen den Mahlzeiten zu nehmen. Da ausreichend Erholung, sprich guter und tiefer Schlaf langfristig für das Muskelwachstum essentiell sind, kann GABA meinerseits als natürliche Entspannungshilfe empfohlen werden. Neben der optimalen Ernährung und gezieltem Training macht ausreichend Regeneration das Trio der Muskelaufbaufaktoren komplett. Was ich aber sehr deutlich feststellen konnte war, dass mein Schlaf tiefer und fester struggle. Ich habe mich trotz teilweise kurzer Nächte (unter 8 Stunden) und auch im Allgemeinen sehr gut ausgeschlafen gefühlt. Das führte dazu, dass weniger Schlaf zur vollständigen Erholung bei mir notwendig war. Es besteht aber die Gefahr bei gleichzeitiger Einnahme von Schlafmitteln -oder Beruhigungsmitteln, dass GABA das Suchtpotential erhöht.
References:
https://elitechefnetwork.co.uk/companies/wachstumshormon-hgh-and-peptide-kaufen-sie-legale-hgh-in-deutschland/
should i use steroids
References:
https://www.naukrikro.com/companies/wachstumshormone-hgh-authorized-kaufen-on-line-rezeptfrei/
It’s worth mentioning that these limits can be increased for
players with VIP status, granting them the opportunity to enjoy even higher withdrawal limits tailored to their exclusive gaming needs.
The three facets of the class as a data type are its name, its relation to other classes, and the names of the slots that make up instances of the class.2 The basic form of a DEFCLASS is quite simple. Python.11 Rather, class-allocated slots are used primarily to save space; if you’re going to create many instances of a class and all instances are going to have a reference to the same object–say, a pool of shared resources–you can save the cost of each instance having its own reference by making the slot class-allocated. Disponible sur ordinateur et mobile, ce slot vous invite à viser les lingots d’or tout en évitant les explosions de TNT à chaque partie. Code that directly accesses the balance slot will likely break if you change the class definition to remove the slot or to store the new list in the old slot. Berkman told HitQuarters he believed what the band needed was a “fifth member to play the guitar and free up the singer, so he could be the star I perceived him to be.” Octone immediately insisted that the band change its name to break with its pop past.
Ahaa, its fastidious discussion on the topic of this paragraph here at this blog, I have read
all that, so now me also commenting here.
order steroids
References:
https://khuranadrivingschool.com/solar-power-in-developing-nations-brightening-lives/
why take steroids
References:
https://paramedical.sureshinternationalcollege.in/diploma-in-veena/
hard rock casino northfield ohio
References:
https://admin.dnn.mn/wp/naadmin-tasalbar-duuschee-dnn-mn/
real money online poker
References:
https://talukadapoli.com/travel/listing/yakub-baba-darga/
Nicely put. Thanks!
Feel free to visit my web page: https://mj-go.kr/bbs/board.php?bo_table=free&wr_id=3310262
Prevention and patient education are essential in efficiently addressing urinary incontinence. Individuals and their families must be notified that although urinary incontinence is extremely common in older adults, it is not a regular component of aging. They must understand that numerous root causes of urinary incontinence are reversible, and all instances are treatable to some degree. A 24-hour or 3-day nullifying diary may be useful in chosen cases. [17] [18] The client is instructed to write down and record the moment and the quantity of urine nullified in mL for a minimum of a full 24 hours. Overactive bladder people have a tendency to nullify in small quantities often throughout the entire period. Patients with international polyuria have actually fairly huge invalidated urine quantities throughout the day and night, with very large complete quantit
However as a health care specialist, my suggestion would certainly be that about every couple of hours you’re altering and making sure that your product is not at capacity. And Quigley’s hip pain was most likely related to her pelvic issues too. ” We have deep hip stability muscle mass that belong to our pelvic floor,” describes Reardon.
Medications For Urge Urinary Incontinence
This can cause urinary incontinence as a result of the stress of fat on your bladder. High-impact workout taxes your pelvic flooring muscles and can boost leakages. Being overweight can weaken your pelvic floor muscular tissues and trigger urinary incontinence due to the pressure of fat on your blad
EMFace. EMFace is just one of the very best skin-tightening treatment alternatives for 2024. It”s a non-surgical face rejuvenation procedure that lowers wrinkles, tightens skin, restores lost quantity by stimulating collagen production, and strengthens underlying face muscle mass that sustain the face.
For example, throughout energetic sporting activities, the strenuous activity and/or the coming with sweat might trigger the tool to come to be dislodged and, consequently, ineffective. The person continues to be dependent on the device indefinitely; when it is eliminated or displaced, the urinary incontinence returns. The most generally utilized pessaries for tension urinary system incontinence are the ring and Gellhorn pessaries.
To estimate the proportion of the treatment group that might not have needed VEL+ UEL treatment, we took a look at those with light intensity. Of the 23 individuals in the therapy group, about 6.64 were approximated to have been treated without treatment based upon the all-natural treatment rate of 28.89% observed in the control team. This equates to an estimated 28.87% of the therapy team potentially not needing the therapy. The mean treatment result of around 11.0 suggests that the therapy group revealed an ordinary improvement of approximately 11 systems compared to the control group. Nonetheless, the huge conventional inconsistency of approximately 14.8 shows substantial irregularity in the treatment results, implying that the choice of covariates substantially influences the outcomes.
Surge In Pelvic Floor Disorder
Pessaries press the urethra closed to assist control pee leak and permit you to urinate typically throughout the day. Some females wear a pessary only when exercising, but others leave it in, depending upon when their signs and symptoms are most bothersome. ” By eliminating these irritants from your diet plan, you lower the swelling activity on the neck of the bladder,” Krisiloff discusses.
Bulking Representatives
The modified R ² for the version was 0.45, indicating that the version discussed 45% of the general variation in data. This suggests that while the design records a substantial part of the variability, various other unmeasured variables might impact the improvement of the 1HrPadTest and Return after one year. Prior to carrying out the regression evaluation, a medical diagnosis of multicollinearity was executed to make sure that too much relationships among variables did not present predisposition right into the outcomes.
Partner With Us To Treat Your Individual’s Cancer
A physical therapist that specializes in pelvic floor disorders can help you master the proper methods. It can take 4 to 6 weeks of normal exercise to see symptoms enhance. With modest to serious anxiety incontinence, you might leak more than a tbsp of urine even during much less arduous tasks like standing or flexing over. Leaking pee when there’s stress on your bladder is the leading sign of stress urinary incontinence. Mild stress and anxiety urinary incontinence may cause you to leakage declines of pee during activities like heavy exercise, giggling, coughing or sneezing. Any individual can have urinary incontinence, but the problem influences twice as many women as g
Some self-help tips and way of life changes can eliminate symptoms of urinary incontinence. If you are ready to find relief from the signs of overactive bladder, connect to your physician or connect with a urology expert today. Age, hormonal changes, obesity and particular foods and beverages can add to bladder overactiv
Placing your home in a trust fund transfers ownership to a firm till
you either vacate or pass away.
Teeth whitening can substantially boost your smile, enhance your appearance, and improve confidence. It favorably affects your self-esteem and general health. Discover the Humana Extend dental strategies, designed to offer thorough coverage for dental, vision, and hearing benefits. These plans cater to consumers seeking inclusive oral care, with choices like protection for dental implants. Motivated by client feedback stressing the value of whole-person care, Humana Extend stands for a transition from conventional oral insurance coverage.
Why Do Dental Braces Discolor Teeth?
The plaque and tatar can weaken the enamel possibly triggering delcalficiation, or white spots, and eventually dental caries. The tartar likewise produces an extra obstacle between the whitening solution and your enamel. This can leave you with darker areas and even more uneven outcomes. Jagged, congested, or spaced-out teeth, overbites, underbites, and crossbites can be properly treated with braces. Correcting bite troubles and stopping future oral problems can enhance on the whole oral wellness. If your gums are undesirable, treat them prior to choosing teeth bleaching.
Its sustained-release potassium nitrate and fluoride formula provides prompt results and is available in both syringes and prefilled non reusable trays. Intrinsic discoloration occurs below the surface of the tooth and can be harder to get rid of, but it can be treated. External discoloration is extra surface-level discoloration and can generally be treated with whitening toothpaste and regular dental cleani
Once it’s harmed, your body can’t regrow it, making preservation crucial. When enamel erodes, your teeth end up being sensitive and susceptible to decay. While these ingredients guarantee a brighter smile, they’re actually damaging your enamel via duplicated chemical exposure. You’re essentially trading long-term oral health for temporary cosmetic advantages. Great deals of things can cause your enamel to fray, like cleaning too hard, grinding your teeth, taking certain medicines or having specific hereditary conditi
Many people can safely utilize lightening products, however it’s important to seek advice from your dental practitioner, specifically if you have delicate teeth or dental job. A lot of non-prescription products are risk-free, but it’s constantly best to speak with your dentist before beginning any type of whitening routine. Additionally, some individuals experience level of sensitivity during or after bleaching treatments. If this occurs, think about using desensitizing tooth paste or taking breaks in between therapies.
Common Causes Of Teeth Discoloring
The natural shade of the teeth differs, not all teeth hues are the same. You may observe that also if you maintain good dental health or prevent staining foods, your teeth remain yellowish. Cigarette smoking and the use of cigarette items are widely known factors to yellowing teeth. The nicotine and tar in cigarettes, cigars, and chewing tobacco can trigger significant discoloration on the teeth. These substances not only darken the enamel yet also bring about the build-up of plaque and tartar, which can further add to discoloration.
Exactly How Do Your Genetics Affect The Shade Of Your Teeth?
You need to likewise practice excellent oral health and visit a dental professional at least twice a year. External discolorations impact the surface area of the enamel, which is the difficult, outermost layer of teeth. Although tooth enamel can be conveniently tarnished, these discolorations can typically be eliminated or corrected.
Actually, researches suggest that almost 90% of grownups experience some form of tooth discoloration over their life time. Way of living behaviors also play an important duty in tooth discoloration. Smoking or using cigarette items results in brown or yellow stains. Poor oral health, characterized by infrequent brushing and flossing, allows plaque accumulation, making discoloration more noticeable.
Dentists may offer in-office or at-home professional teeth bleaching treatments. These approaches utilize hydrogen peroxide or carbamide peroxide to break up stains and lift them from your teeth. Expert lightening works best on surface area (external) stains. Yet some whitening items can get rid of deep oral (innate) spots, also. Tooth staining refers to the discoloration or darkening of your teeth.
Prior to we look into whitening techniques, it’s necessary to understand why teeth blemish. While genetics can play a role– some individuals normally have thicker enamel that appears whiter– most staining comes from way of life selections. Elements such as diet, dental health, and also specific drugs can add to yellowing teeth. As an example, beverages like coffee, tea, and red wine are infamous for discoloring enamel gradually. Understanding your one-of-a-kind dental demands is vital in combating teeth discolorations and keeping total oral health and welln
This nutrient is a potent antioxidant, able to combat totally free radicals created by the sun.
poker bonus no deposit
References:
https://parwins-hairsalon.de
titan casino
References:
aurousseauarchitecte.com
sands casino reno
References:
super-fisher.ru
2ahukewjkv_v5usvnahvlip4khu09akmq420oa3oecakqcq|the best steroids for muscle
growth
References:
sehiyyetv.az
all of the following are common side-effects of ingesting anabolic steroids except:
References:
gbx9.com
My coder is trying to persuade me to move to .net from PHP.
I have always disliked the idea because of the costs.
But he’s tryiong none the less. I’ve been using Movable-type on numerous websites
for about a year and am nervous about switching
to another platform. I have heard good things about blogengine.net.
Is there a way I can transfer all my wordpress content into it?
Any help would be greatly appreciated!
Thanks on your marvelous posting! I quite enjoyed reading it, you’re a great author.
I will ensure that I bookmark your blog and will eventually come back someday.
I want to encourage you to ultimately continue your great work, have
a nice holiday weekend!
holland casino vacatures
References:
https://Eazyworldtour.Com/Product/Switzerland-And-Austria-2025-Onward/
Due to its sturdy encryption, monetary information is very protected on PayPal and the service is straightforward to make use
of, which is why so many people worldwide use it daily.
As of 2020, PayPal operates in more than 200 countries
and has over 300M registered accounts. PayPal permits
clients to send, receive and hold funds in additional than 20 currencies
worldwide. As for real money gambling sites, the variety of online
PayPal casinos is continually growing. PayPal deposits
happen instantly, and withdrawals are often processed inside 24 hours, generally even inside
minutes. On prime of that, it provides an extra layer of security by keeping your bank or card details
personal.
Withdrawals are usually processed inside 24 hours, so you can access your winnings shortly.
Sure, PayPal makes use of SSL encryption, does not share your financial institution knowledge, and has cost safety.
Since PayPal has expanded to cowl all online markets, together with gambling, it is
become extremely popular as a casino payment method.
Immediate PayPal On Line Casino withdrawals are one of the greatest advantages of using
this payment technique. From the outcomes of our first-hand
tests, listed under are our top 5 best immediate PayPal withdrawal
casinos in the USA. It is essentially like having a financial
account solely for on-line gambling purposes, offering you
with more control over your spending.
Users can link their bank accounts to PayPal for seamless transactions, making it easier to deposit and withdraw funds.
Payments are transacted utilizing only an email tackle, making anonymity one of the major points of interest for customers.
PayPal is a trusted and safe means of making deposits and withdrawals at reputable on-line casinos.
This article will assist you to find the best PayPal on line casino choices, highlighting
top-rated online casinos that facilitate swift deposits and withdrawals, low fees,
and a robust gaming choice. As A Outcome Of of the protection and security that’s PayPal,
many casinos goal to obtain the brand, providing it as a method to transact online.
We check out a variety of the highlights of PayPal casinos and invite you to take a look with us.
PayPal casinos, including desk video games, stay vendor video games,
slots, Megaway video games, and more. Canadian casino
gamers can maintain up to date with all their on-line playing choices through our online on line casino Canada tracker, while we have also
obtained a devoted on-line on line casino Ontario web
page. As a trusted supply of on-line playing data for greater
than 28 years, we remain dedicated to reviewing and recommending the most reputable and protected gambling sites.
Depositing with PayPal is simple and supported by many legal US on line casino websites.
As Soon As your PayPal account is ready up and
linked to a cost source, you can transfer funds into your on line casino stability in just some
steps. Sure, you presumably can play and win real cash at an online casino, so long as the casino pays out in your currency.
Every on line casino on this list was carefully chosen utilizing benchmarks
that matter to actual players.
You Will additionally discover Caesars Palace On-line On Line Casino on our record of the most effective online
free spins casinos. You’ve landed on the proper page if you’re an internet casino player looking for the most effective PayPal-accepting sites.
On this web page, you’ll find unbiased on line
casino evaluations from trade specialists of the most effective real cash casinos that
accept PayPal transactions. Punters who play at online casinos
have entry to essentially the most environment friendly banking selections because of PayPal, which is a dependable and risk-free technique
for making deposits and the most secure. Its customers’ protection and
security are usually prioritized at online casino paypal casinos that settle for
PayPal as a cost method. Once More, not all on-line casinos accept PayPal as
a deposit or a withdrawal method. Players are inspired to check the casino’s web site to see if it supplies them with entry to the fee
resolution.
The app processes over $1 billion in annual player payouts across
legal US states. Mobile online casino actual money browser video games offer prompt access with out app downloads, good for infrequent
gamers or restricted storage units. HTML5 technology delivers native app-like efficiency via cell browsers with automated updates and cross-platform compatibility.
Browser casinos help all devices with fashionable
net browsers together with iOS Safari, Chrome, and Firefox.
Real cash cellular casinos present genuine gambling experiences
with cash prizes, regulated gameplay, and professional
customer help. Whereas free casino apps offer entertainment worth, solely licensed mobile casinos
for real cash ship the authentic thrill of profitable precise money prizes.
Our list of PayPal casinos permits you to browse just on line casino websites that accept PayPal.
That said, PayPal doesn’t permit funds to or from
on-line casinos in numerous countries, so it also depends on your country
of residence. BetMGM is the best PayPal on line casino web site that
U.S. players can enroll with right now. It provides a huge
number of high quality games, the software is superb, payouts are reliable and
there are many appealing promotions.
Look for comprehensive FAQ sections, video tutorials, and dedicated cellular help options inside the app.
On-line since 2016, Websweeps offers 500+ sweepstakes slots, video poker,
and Plinko; accepted payments include Visa, Mastercard,
Skrill, PayPal, and bank wire transfer. Fortune Wheelz Casino opened in 2023, offering 600+ slots, day
by day wheel spins, and instant-win games; payments assist Visa, Mastercard, PayPal, Google Pay,
and Bitcoin. Novibet Casino opened its digital doorways in 2010, providing
3,500+ slots from Pragmatic Play and Pink Tiger, live Sic Bo and baccarat tables, and a devoted virtual-sports lobby.
Accepted funds include Visa, Mastercard, Skrill,
Neteller, Paysafecard, and prompt financial institution transfer.
Jackpot Metropolis Casino launched in 1998 and
today hosts over 1,200 Microgaming and NetEnt slots, progressive jackpots, virtual table games, and Evolution live-dealer blackjack and
roulette.
Der Stoffwechsel wird angekurbelt, was die Fettverbrennung beschleunigt.
Legale Steroide können direkt über die offiziellen Webseiten der
Hersteller wie CrazyBulk oder über autorisierte Online-Händler gekauft werden,
wobei der Direktkauf beim Hersteller oft Qualitätsgarantien und Rabattaktionen bietet.
Erkennungszeichen seriöser Anbieter sind oft Gütesiegel,
die geprüfte Qualität und Zuverlässigkeit signalisieren, während
Vorsicht bei unbekannten Plattformen geboten ist, die häufig Fälschungen verkaufen. Die Wahl des richtigen Produkts und der sichere Kauf sind entscheidend beim Erwerb von legalen Steroiden. Hier erfährst du, wie du seriöse
Anbieter erkennen kannst und was es mit der Verfügbarkeit ohne Rezept auf sich hat.
Einhaltung der vom Hersteller angegebenen Tagesdosis ist Pflicht, um auf
der sicheren Seite zu bleiben und unerwünschte Wirkungen zu vermeiden, da
Überdosierungen keine besseren Resultate liefern.
Hier setzen HGH Booster an und machen sich diese Aminosäuren zunutze,
um die menschliche Wachstumshormonproduktion in Ihrem Körper anzukurbeln. Wachstumshormone,
die man noch HGH nennt, sind die Hormone, die sehr stark sind und die für denMuskelaufbau verantwortlich sind.
HGH ist noch stärker als Testosteron Produkte, denn es ist dasMasterhormon im unseren Organismus und es kontrolliert alle Wachstumsprozesse.
Wachstumshormon ist Peptidhormon, das wichtig für Wiederherstellung,
das Wachstum und fürFortpflanzung von Zellen im Körper
ist.
Testosteron Booster wie Ashwagandha und Ginseng wiederum optimieren den Hormonspiegel für maximales Wachstum
von Muskelmasse. Dieser Arzt/Wissenschaftler befürwortet
oder befürwortet in keiner Weise den Kauf, Verkauf oder die Verwendung dieses Produkts aus
irgendeinem Grund. Polypeptide.ltd steht in keiner stillschweigenden oder sonstigen Verbindung
oder Beziehung zu diesem Arzt. Der Zweck der Erwähnung dieses Arztes besteht darin, die umfassende Forschungs- und Entwicklungsarbeit der
an diesem Peptid arbeitenden Wissenschaftler anzuerkennen, anzuerkennen und zu loben.
D-Bal MAX bietet eine sichere Different zum traditionellen anabolen Steroid Dianabol.
Ohne rechtliche Sorgen können Athleten ihre Muskeln stärken und ihre Kraft steigern. Dr.
Jean Zeng hat an der Fakultät für Biowissenschaften und Medizin des
King’s School London studiert. Der Autor dieses Artikels
empfiehlt nicht den Kauf von HGH (Human Progress
Hormone). Wenn Sie etwas kaufen möchten, wenden Sie sich bitte an den Kundendienstmitarbeiter.
Aber wie bei allen Medikamenten kann HGH auch Nebenwirkungen haben.
Darüber hinaus können Hormonbooster den Aufbau von Muskelmasse und den Abbau von Körperfett unterstützen. Einige von ihnen können auch die kognitiven Fähigkeiten positiv beeinflussen und die Libido steigern. Es ist ein wünschenswertes
Hormon, besonders bei Sportlern, da es die Entwicklung von Muskelmasse
fördern und die Regeneration des Körpers nach körperlicher Anstrengung unterstützen kann.
Gleichzeitig kann der Wachstumshormon-Booster die Optimierung des Schlafes beeinflussen und
seine Qualität verbessern, sowie die Verbesserung des Zustands von Haut
und Haaren. Testosteron ist besonders wichtig für den Aufbau von Muskelmasse – es kann anabol wirken und Muskelwachstum ermöglichen.
Das Hormon kann jedoch auch die Ausdauer und Health bei körperlicher
Anstrengung, Libido und Fruchtbarkeit bei Männern beeinflussen und die Konzentration verbessern.
Es kann in Apotheken mit einem Rezept gekauft werden, oder Sie können es online direkt auf unserer Web Site kaufen. Bei Erwachsenen kann es
sich auf die Muskelmasse und -kraft, die Knochendichte und die Hautelastizität auswirken, aber
es ist nicht geeignet, die Körpergröße zu erhöhen.
Wir empfehlen jedoch, das Hormon so lange wie möglich
im Kühlschrank aufzubewahren, bevor es aufgelöst wird, und immer im Kühlschrank, wenn es aufgelöst ist.
Die Hormone, die Sie in VERMODJE finden, werden unter gekühlten Bedingungen und gemäß allen Anforderungen gelagert, was garantiert, dass das Produkt Sie in seiner ursprünglichen Kind und mit seinem vollen Potenzial erreicht.
Somatropin wird in Type einer trockenen Lösung und separatem bakteriostatischen Wasser für seine Auflösung geliefert.
Wenn das Hormon nicht aufgelöst ist, ist es viel stabiler, so dass es nicht im Kühlschrank aufbewahrt werden muss
und problemlos einen oder mehrere Tage lang von uns zu Ihnen reisen kann.
Mit den genannten Tipps, kannst du deinen HGH-Wert ziemlich einfach steigern.
Ribose ist weiterhin in der Lage Trainingsleistungen zu verbessern, Stress zu verringern und das gesunde Niveau von Herz und Muskeln zu
unterstützen und zu erhalten. Beta-Alanin ist wiederum eine nicht-proteinogene Aminosäure, die
sich besonders in den vergangenen Jahren bei Ausdauer orientierten Sportarten, wie Basketball durchgesetzt hat(13).
Zu finden ist Beta-Alanin überwiegend in Pre Exercise Supplementierungen, die es im Handel entweder,
als Tabletten in Pulver-oder in kapselform zu kaufen gibt.
L-Glutamin ist wiederum eine Aminosäure, gehört zu den nicht essentiellen Säuren und kann vom Körper
selber produziert werden.
Ja, guter Schlaf, regelmäßige Bewegung, eine ausgewogene
Ernährung usw. ③HGH-Ergänzung und orales HGH, ihre Wirkstoffe sind
alle Roh-HGH-Pulver. Laut HGH-Studien ist die beste Verabreichungsmethode
für HGH die Injektion, da orales HGH erst vom Magen verdaut wird, bevor
Ihr Körper davon profitieren kann. Bevor Sie mit der Einnahme von Hormonersatzmedikamenten beginnen, ist es wichtig, mit einem medizinischen Experten zu sprechen. Sie können Sie
beraten, ob eine HGH- oder Testosterontherapie für Sie geeignet ist, und Ihnen die möglichen Gefahren und Vorteile erläutern. Testosteron ist das Haupthormon, das für die Entwicklung
männlicher Sexualmerkmale wie Muskelwachstum, Körperbehaarung und eine tiefe Stimme verantwortlich ist.
Es hilft auch, die Stimmung, die Knochendichte und das allgemeine Energieniveau zu regulieren.
Sie stimulieren nicht nur die Produktion von IGF-1 (insulinähnlicher
Wachstumsfaktor), sondern erhöhen gleichzeitig auch die Proteinbildung sowie die Konzentration von Glukose und freien Fettsäuren.
Wichtig ist, dass HGH (menschliches Wachstumshormon) mehrere Gewebe
im Körper beeinflusst und die Knochen- und Knorpelbildung bei Kindern und Jugendlichen fördert.
HGH Droge sind völlig legale HGH Medikamente, die bedenkenlos HGH kaufen werden dürfen und keine HGH Nebenwirkungen haben. Im Store sind nur legale Wachstumshormon HGH Artikel erhältlich, die problemlos gekauft werden können. Die Peptidbehandlung signalisiert
die Freisetzung der körpereigenen natürlichen Synthese
des menschlichen Wachstumshormons HGH und simuliert die Funktion, die
Peptide im Körper ausüben. Es gibt Wege die Wachstumshormone auf
natürliche Weise zu steigern.
Dabei sollten der GoQuick-Fertigpen im GoQuick-Umkarton oder die Zweikammerpatrone im
Umkarton des Pens aufbewahrt werden, um den Inhalt vor Licht
zu schützen. Die Gebrauchsanweisung für die Anwendung des GoQuick®-Fertigpens finden Sie
am Ende dieser Packungsbeilage. Eine sehr seltene Nebenwirkung, die wegen des Konservierungsmittels Metacresol auftreten kann, ist eine Muskelentzündung in der Nähe der Einstichstelle.
Wenn Ihr Arzt bestätigt, dass das bei Ihnen aufgetreten ist, sollten Sie
eine Genotropin-Zubereitung ohne Metacresol verwenden. Bildung von Antikörpern gegen das verabreichte Wachstumshormon, doch scheinen diese die Wirkung des Wachstumshormons nicht zu beeinträchtigen. Die sehr häufigen und häufigen Nebenwirkungen können bei
Erwachsenen in den ersten Behandlungsmonaten einsetzen und entweder spontan oder nach
Dosisverringerung abklingen. Hierfür bietet sich das Zubettgehen an, weil man sich leicht daran erinnert.
References:
oral (https://carolarinker.de/wp-content/pgs/hgh_Kaufen_1.html)
Following common sense guidelines may also help defend your liver
during a Winstrol cycle – keep away from all alcohol and take a glance at not to
use any medications except essential, as many are also
liver-toxic. However Masteron is the better all-around cutting
steroid and the one you must use if you would like to run an extended minimize.
Save Winstrol for the ultimate weeks earlier than a contest, where it
excels.
This is a dramatic increase, considering most bodybuilders might be in a calorie deficit when taking this
steroid and thus are aiming to easily maintain their
strength. In this comprehensive review, we delve into the workings of Winstrol, a
famend anabolic steroid widely recognized for its muscle-enhancing properties.
Beyond its muscle-building benefits, Winstrol demonstrates efficacy in treating varied situations such as angioedema and stroke, thereby mitigating the chance of severe health ailments.
As a steroid that does not aromatize there might be no water
retention but the “dry feeling” will not be what many
think it’s. Most who use the steroid might be physique athletes or health
club rats throughout a slicing phase. They may also sometimes add
it right into a plan late within the food plan as quickly as they’re
already lean. Usually, if you turn into very lean, bodybuilding
lean, this makes the joints slightly uncomfortable.
As for professional athletes who have nearly every final steroid at their disposal, remember,
if Winstrol weren’t efficient in competitive sports so many athletes
wouldn’t make it a major and favorite selection. In fact, the combo of Winstrol with low doses of
Nandrolone is a very common stack among many athletes,
and this stack will greatly eliminate any potential joint discomfort should it exist.
So, if you have any pre-existing joint situations – I
would recommend towards taking it. It’s not a model new factor that steroids include a plethora of side effects.
As a result, it’s typically utilized by powerlifters and different
athletes who want to add strength with out rising their measurement.
In this weblog post, we’ll discuss the pros and cons of each steroid,
so that you can make an knowledgeable choice about which one is right
for you. Finally, the question of which one is best comes all the means down to
which one can be better for you.
In distinction, whenever you swallow most steroids, an enzyme in your liver called
17beta-hydroxysteroid dehydrogenase (17beta-HSD) breaks them down. Even should you took a whole bottle of testosterone tablets, only a tiny fraction would enter your bloodstream—probably not sufficient to fail a drug test.
By decreasing SHBG ranges within the blood, Winstrol makes the opposite steroids you’re taking stronger, too.
Nonetheless, it’s nonetheless a helpful start line for estimating a
steroid’s muscle-building potential versus its unwanted aspect effects.
Winstrol, on this regard, is the alternative of Deca Durabolin, which
might really enhance joint well being due to elevated manufacturing of synovial
fluid. TUDCA is an FDA-approved remedy for varied cholestatic liver ailments (2).
Although Winstrol is predominantly used as a cutting agent, its anabolic results and ability to add lean mass should not be underestimated.
Nonetheless, if you’re one of the unfortunate ones with genetics working in opposition to you, then you can expect to be coping with some of
these well-known steroid side effects caused by Winstrol’s androgenic exercise.
Winstrol is a DHT-derived steroid, and in distinction to steroids that
are based on the testosterone hormone, DHT-based steroids cannot be transformed into
estrogen. This means Stanozolol comes with no
estrogen-related side effects in any respect. It’s harsher than some of the other popular chopping steroids,
and most users will battle with one type of facet effect or
one other.
Alternatively, if customers would like to cycle
winstrol with fewer side effects (than the above cycle), 8-10mg per day can be taken for 6 weeks.
If you go longer than that, you’re risking excessively excessive LDL cholesterol levels.
Nonetheless, if somebody was a novice to steroids, and ran a
winstrol cycle, their strength would still go through the roof.
As I mentioned, Anavar is among the few steroids ladies can confidently use.
Cycles must be restricted to six weeks, and the dosage must be 10mg
daily. Some women may want to go further and add another two weeks to the cycle whereas increasing the dosage for those last two weeks as much as 20mg daily,
however monitor for any potential unwanted effects. The lack of danger of water retention is a
serious advantage of Anavar and an enormous
cause why it’s such a well-liked and potent chopping compound, together with for competitive customers.
How much physique fat may be lost is dependent upon your current body composition; Anavar shouldn’t be considered a magic
weight reduction capsule.
Winstrol, also referred to as Stanozolol, is a synthetic
anabolic steroid that was first developed in 1962.
Newbies should start with decrease doses to evaluate
tolerance and keep away from extreme unwanted facet effects.
Dosages usually range from 50mg to 100mg daily, depending on the cycle size and user
objectives. Oral varieties are common, while injectable variants might have different administration protocols.
If gamers need different types of high-limit playing,
they need to strive the Palazzo High-Limit Gaming Lounge at the
Venetian. It has sixty seven of the most recent high-stakes slots, plus the ability to play high-roller versions of craps,
roulette, Tiger Baccarat, and Ultimate Texas Hold’em.
The latter sport is linked to the Millionaire Progressive, a popular facet guess that’s
made eleven millionaires in its time. When they gamble big
sums of money, they win with comps and cashback even if
the gaming session doesn’t pay out a lot.
These sites all come with truthful wagering requirements and provide bonuses that make
it easy so that you simply can earn a ton of cash while
wagering on-line. One frequent query that usually arises when discussing high roller casinos
is how the video games work in these sites and how they’re totally different from their low-roller counterparts.
In fact, some video games have different variations the place one version accepts small wagers whereas the
opposite has a loopy excessive restrict. The prime high roller
casinos typically function video games made by one of the best online casino
developers in the industry. This is certainly one of the primary advantages
of taking part in in considered one of these websites – you’ll be capable of
place extremely massive wagers and count on an honest sum of money in return when you handle to win. Anyone signing up
on the really helpful casinos for high rollers in the USA will immediately be treated like a VIP.
Look for respected on-line casinos that provide unique bonuses
for high-stakes gamers. John Ford has been writing on-line gambling
content for over 18 years. Born and raised in the coronary heart of the Short Pump, Virginia, John’s journey by
way of the on line casino business started on the on line
casino floor itself. He started as a supplier in numerous games, including blackjack, poker, and baccarat, cultivating an understanding that only
hands-on expertise can present. John’s ardour for writing casino guides
stems from his casino expertise and his ardour for helping fellow punters.
All the most effective online on line casino sites
provide generous deposit bonuses for their prospects.
Apart From a welcome bonus, you can even get
other exciting presents to grab free spins, get cashback, or take part in thrilling VIP packages.
When creating the listing of the highest 10 actual cash casinos, we paid
probably the most consideration to the gaming portfolio.
Games are the center of on-line casinos, and with out them, you won’t be capable of enjoy a lot.
It just isn’t unusual for a casino to extend sure amenities to a excessive roller that frequents the ability.
Since the excessive curler spends a substantial amount
of money in the on line casino, the house owners will typically
provide free foods and drinks while the person is taking half in the games.
This investment by the 888 casino Bonus – blackcoin.co,
costs very little, and the chances for incomes quite so much of cash
from the high roller take some time very worthwhile.
PokerNews activates MyStack for every WSOP event, regardless of that match’s buy-in, allowing you to immediately modify your chip counts in our reside reporting.
To make it even simpler for you, we now have ready a step-by-step information that you can use to enroll at your
online casino of alternative. You can browse all of the titles using iOS and Android gadgets with none issues.
Just seize your telephone, open the cell browser, and log
into your account. You should make a minimum deposit of $20 for bank cards, $10
for cryptos, and $10 for player transfers. The common withdrawal time is as much as 1 hour though fiat can take up to forty eight hours.
If you don’t know the place to begin out, ensure you take a look
at HighRoller. This is the highest online casino, thanks to its great choice of jackpot
slots, a beneficiant welcome bonus, and excellent cellular compatibility.
Each of these games have a 99% to ninety nine.8%% RTP, meaning you’ll have
an opportunity of profitable each hand.
This privateness provides to the mystique – the “mysterious millionaire betting millions” – nevertheless it additionally means whales don’t get the normal social fun of
a day at the sportsbook. The energy a whale wields comes from the
menace of taking their motion elsewhere. Las Vegas, Macau, Monte Carlo – these playing hubs are in a constant arms race to draw
whales with bigger and better perks. In the old days, a whale who blew $500,000 at baccarat would get far more fanfare than someone who
bet $500,000 on the Super Bowl. Sports betting whales flew a
bit under the radar, in part as a end result of sportsbooks operated on thinner margins and didn’t want to lose huge.
The more you bet, the more you’re more doubtless to obtain invites to special promotions,
larger stakes games, and personal areas where the
stakes are even more elevated. Casinos usually acknowledge
high rollers via their betting patterns. They could then prolong invites to
VIP golf equipment, provide private hosts, and provide unique bonuses or rewards.
To increase your chances of changing into a excessive roller, you
may need to satisfy sure spending thresholds or demonstrate your willingness to guess massive
sums over time.
It only takes you a couple of hours to understand
even essentially the most complex playing methods.
That is why tens of millions of gamblers around the globe are wagering exorbitant quantities of money into the game every day.
High-roller slots often have greater RTPs and greater jackpots compared to regular slots.
A sharp may guess $5,000 on a sport where they see a transparent edge and
skip the games where they don’t. They would possibly grind
out earnings over the long term, treating it like a
severe investment. Many whales are actually not very expert at
selecting winners – they could even be pretty unhealthy, dropping
more typically than they win. They can afford to lose and
hold taking part in, so they’re much less disciplined about in search of value
within the odds. Daniel Smyth has seen the web poker, on line casino, and betting business from every angle.
He previously played poker semi-professionally before
working at WPT Magazine as a writer and editor.
70918248
References:
steroids and muscle growth – Jeanett –
70918248
References:
anabolic steroids shop (petratungarden.se)
70918248
References:
dbol steroid side Effects (super-fisher.ru)
70918248
References:
Strongest Legal Steroid (https://Www.Trefpuntstan.Be)
Coupling this with common cardiovascular exercise can be beneficial in sustaining a more healthy ldl
cholesterol balance. How Winstrol makes you’re feeling after administration can differ
based mostly on individual experiences, private tolerance
levels, and the dosages taken. It is essential to maintain in thoughts that each
person’s response may differ, but there are some common sensations reported by
Winstrol customers. Hair loss, especially in individuals genetically predisposed to male sample baldness, is one other
potential aspect impact of Winstrol. The conversion of testosterone to dihydrotestosterone (DHT) can speed up hair loss in vulnerable individuals.
How quick Winstrol works, causing peak serum testosterone levels, will rely
upon the strategy of administration. Thus, oral Winstrol is extra
simply damaged down and cleared by the physique; thus, more regular dosing is
required to maintain up peak serum testosterone.
Thus, if someone is regularly utilizing Winstrol for cutting, it
may be beneficial to make the most of Deca Durabolin in off-season bulking stacks to
guard their joints long-term. Fats loss and reductions in extracellular
fluid will both promote a extra vascular and outlined physique.
Our staff of medical specialists are there for you in each step of the way, from discovering the
proper doctor and hospital to any kind of assistance.
Still, it is crucial to contemplate its unwanted
effects like lowered sperm count in nearly 59% of customers.
In the fitness world, it’s celebrated for enhancing lean muscle
growth and helping with fats loss. In this weblog post, we’ll dive into the world of Winstrol for bulking cycles.
You’ll learn to incorporate Winstrol into your bulking cycle, the benefits of doing so, and tips
on how to maximize your positive aspects. We’ll also discover some
common misconceptions about Winstrol and bulking.
The fastest-acting kind is Tren Acetate, which starts taking impact rapidly as soon as
injected and leaves the body quicker than Tren enanthate.
Muscle gains with the slow-acting Nandrolone decanoate take time to develop,
and customers shouldn’t count on notable features inside the first
weeks of a cycle. A cycle size of no less than 12 weeks is required to get the maximum
benefit from this steroid. While they share comparable anabolic benefits, the greatest way they perform on a cellular stage differs barely, making
every compound more appropriate for different
objectives. Cutting cycles are a critical section in bodybuilding the
place the primary goal is to reduce back body fat while maintaining lean muscle mass.
Sometimes, this section follows a bulking phase—a interval centered on muscle and energy gain. In contrast,
cutting phases emphasize diet, training, and strategic supplementation to disclose muscle definition and vascularity.
First and foremost, it’s important to provide the
body sufficient time to recover between cycles. This
will allow the physique to naturally restore its
hormonal stability and reduce the danger of long-term unwanted effects.
Moreover, incorporating pure supplements into your post-Winstrol therapy routine can further help
recovery and hormonal balance.
Customers report a positive experience, with notable enhancements in their physical efficiency.
Nevertheless, it is very important cycle the product to
avoid long-term use and potential side effects.
Total, Winstrol is a dependable and efficient complement for
these trying to maximize their health outcomes.
The first is a slicing cycle the place you eat in a
calorie deficit and use trenbolone to assist burn fats and preserve muscle.
The Trenbolone slicing cycle entails using trenbolone in combination with different steroids
similar to Winstrol and Anavar. So, if you’re going to take it – make sure to
get your liver checked frequently. As a end result, Dianabol is often utilized by bodybuilders and other athletes who
want to add both measurement and power.
Take A Look At Enanthate is most commonly injected as soon as weekly; however, this
frequency can enhance with larger doses.
Deca is considered one of my go-to compounds that’s highly
effective and rarely faked. Many alternative merchandise
can offer related results to Deca whereas eliminating the concern concerning the scary unwanted effects and health dangers.
Look no further than Deca-Max if you’d like the premier pure, protected, risk-free Deca-Durabolin replacement.
Whereas every individual may have cardiovascular threat components, Deca-Durabolin is considered as having less cardiovascular stress than oral steroids however extra so than regular testosterone.
One of the massive positives of Deca-Durabolin is its lack of
toxicity in the liver.
References:
JBHNews
Oxandrolona authentic,winstrol comprar on line,comprar dianabol en peru,donde.
Creatina bsn, dianabol original price venta de esteroides en mexico df.
Winstrol o dianabol, esteroides legales a la
venta suplementos para culturismo.. Comprar dianabol chile, clembuterol comprimidos comprar winstrol depot.
Una cura de four semanas ideal para ganar masa magra de calidad
con los esteroides orales Dianabol y Winstrol. Winstrol en madrid,
donde comprar esteroides anabolicos argentina,comprar.
Antes del uso de Winstrol, los usuarios suelen tener niveles de
masa muscular más bajos y retención de agua moderada. Al
ver qué hace el Winstrol, generalmente se busca aumentar la definición muscular y mejorar la fuerza sin ganar peso
adicional en agua. Durante el ciclo de Winstrol culturismo, los usuarios pueden experimentar un aumento en la vascularización,
mayor dureza muscular y una apariencia más
definida. Para periodos de definición se puede combinar
con decadurabolin, boldenona o primobolan,
oxandrolona y los resultados van a ser los esperados en cuanto a dureza y rocosidad se refiere.
Es claro advertir que un ciclo con este esteroide no debería sobrepasar las
seis u ocho semanas.
Dianabol se considera un esteroide de aumento de volumen y solo debe
usarse en incrementos de ciclo de cuatro a seis semanas. La hormona primaria que se produce
a partir de este esteroide es la testosterona. Es
uno de los esteroides anabólicos más conocidos y en muchos sentidos es un esteroide anabólico bastante suave que puede ser utilizado con seguridad tanto por hombres como por mujeres.
En hombres, se aconseja tomar entre 25 mg y a hundred mg por
día, de las tabletas orales, durante un período de mes y medio
o dos meses. Sin embargo, en mujeres la dosis se scale back a 5 o 10 mg al día durante 5 a 7 semanas.
Si lo adquieres inyectable, las dosis deberán reducirse puesto que los niveles son más
altos y el efecto es más directo. También aumenta la resistencia al crear glóbulos rojos
que transportan el oxígeno tanto al cerebro como a los músculos.
Este es un ciclo estándar que es suficiente para permitir que los niveles normales de testosterona vuelvan a la normalidad.
Por lo tanto, se requiere realizar una terapia posterior al ciclo al
last del ciclo de Tbol. Cuando realiza PCT al final del ciclo de esteroides,
puede ayudarlo a restaurar el nivel pure de testosterona
y devolver su cuerpo a su estado regular. Generalmente, la
PCT se realiza con los medicamentos más comunes, como Nolvadex, Clomid
y HCG.
Solo te pido que tomes todas las medidas preventivas y estés consciente y preparado para afrontar cualquier circunstancia.
Lo más recomendable es que inicies tu programa de esteroides con un máximo de 14% de grasa
corporal. Si estás por encima de ese nivel deberás entrar en el rango apropiado por ejercicios y
dieta.
Deben detenerse antes de un ciclo regular debido a los problemas de
hepatotoxicidad, y solo se puede ejecutar un compuesto en un momento
dado, esteroide que se utilizan poco. La combinacion de dos o mas esteroides anabolicos orales es una forma
segura de condenar el higado a un ambiente altamente toxico y
poco saludable. No se debe apilar mas de un esteroide oral en un momento dado, incluso dentro de los ciclos de esteroides anabolicos adecuadamente estructurados.
Sin embargo, es importante tener en cuenta que el Dianabol puede provocar retención de líquidos,
lo que puede hacer que los músculos parezcan más grandes pero no necesariamente más definidos.
Estas sustancias pueden ser detectadas en la orina hasta 6 meses despues de su consumo, comprar testosterona comprimido..
Sobre los efectos adversos, no se dan en todas las personas, ni con la misma intensidad.
En ocasiones se puede producir una reaccion alergica
local, expresada en forma de picor, erupcion, piel
roja, and so forth. En caso de que persista hay que consultar con el medico, comprar
testosterona comprimido. Es necesario seguir las recomendaciones del medico sobre la forma de aplicacion.
Por lo general, se necesitan al menos unas pocas semanas antes de que los usuarios
puedan notar una disminución en la grasa corporal y un aumento
en la definición muscular. Además de la fuerza, el Dianabol también puede aumentar la masa muscular.
Los usuarios pueden notar un aumento en el tamaño de sus músculos, especialmente en la zona del pecho
y los brazos.
Al igual que con todos los esteroides orales, los efectos tóxicos en el hígado
hacen que sea inadecuado y potencialmente peligroso tomarlo
durante más de eight semanas. Winstrol es un esteroide muy
well-liked que, a diferencia de muchos esteroides
anabólicos , se usa principalmente para mejorar el físico, el
rendimiento atlético y la fuerza en lugar de aumentar el volumen. How to administer winstrol ordenar legales anabólicos esteroide suplementos para
culturismo. Ambos promueven la masa muscular magra, disminuyen las grasas corporales y permiten ganar más fuerza.
Turinabol es el esteroide anabólico oral más potente con una historia única.
Barato precio comprar legales anabólicos esteroide envío mundial.
Tanto la Azatioprina como la Mercaptopurina son farmacos de accion lenta , es
decir, se debe esperar unos 3- four meses antes de que podamos obtener su maximo efecto.
En caso de que el farmaco se administre en forma de comprimidos y/o
Capsulas (https://Politecnicotafalla.Educacion.Navarra.Es/Web/Pgs/?Comprar_Dianabol_2.Html), se recomienda tomarlos enteros con un vaso de agua, evitando
machacarlos o triturarlos. Su uso en personas con VIH, es para mejorar el desgaste corporal
causado por el virus y se tiene que diferenciar de
los esteroides que se utilizan por su. Se usa solo en pacientes de bajo riesgo (no trombopenicos) y asociado
a ciclosporina u otro inmunosupresor en los de alto riesgo, se
puede tomar clembuterol con.
Очень познавательная статья о создании индивидуальных проектов!
Я давно интересуюсь эта тема, и
радует, что есть компании, которые подходят к этому вопросу так ответственно.
Меня заинтересовал индивидуальный подход Stroyplans к каждому
проекту. Думаю, это важнейший аспект в создании
дома мечты.
Кстати, на днях наткнулся на их сайт https://www.longisland.com/profile/timlarsen964273, там есть много
интересных образцы проектов. Рекомендую заглянуть всем,
кто задумывается о проектировании собственного дома.
Благодарю за такой подробный материал!
Thank you for the good writeup. It in fact was a amusement account it.
Look advanced to far added agreeable from you! However, how can we communicate?
Here is my blog; สล็อตเครดิตฟรี
Wow, amazing blog format! How lengthy have you ever been running
a blog for? you make blogging glance easy. The overall look of your web site is magnificent,
let alone the content!
Here is my web page: HUC99