Basic PWM Design
Pulse width modulation is used in a variety of applications including sophisticated control circuitry. A common way we use them is to control dimming of RGB LEDs or to control the direction of a servo. We can accomplish a range of results in both applications because pulse width modulation allows us to vary how much time the signal is high in an analog fashion. While the signal can only be high (usually 5V) or low (ground) at any time, we can change the proportion of time the signal is high compared to when it is low over a consistent time interval.
When the signal is high, we call this “on time”. To describe the amount of “on time” , we use the concept of duty cycle. Duty cycle is measured in percentage. The percentage duty cycle specifically describes the percentage of time a digital signal is on over an interval or period of time. This period is the inverse of the frequency of the waveform.
If a digital signal spends half of the time on and the other half off, we would say the digital signal has a duty cycle of 50% and resembles an ideal square wave. If the percentage is higher than 50%, the digital signal spends more time in the high state than the low state and vice versa if the duty cycle is less than 50%. Here is a graph that illustrates these three scenarios:
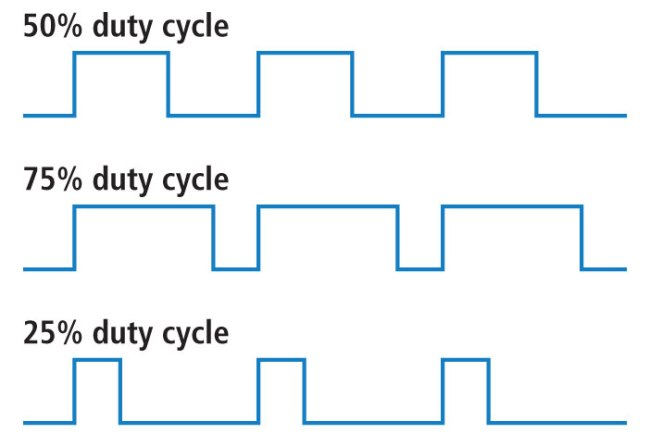
To learn more https://learn.sparkfun.com/tutorials/pulse-width-modulation/all
The circuit
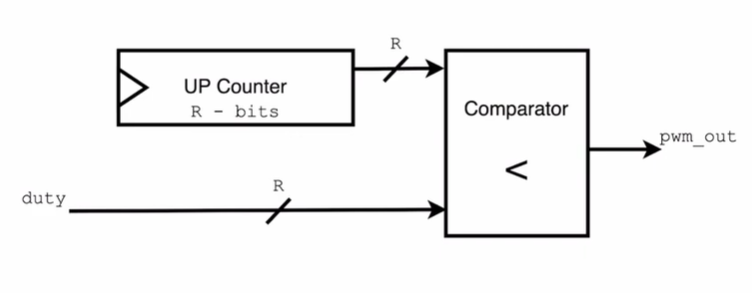
- Components: The design comprises two main components: an up counter and a comparator. The up counter is typically an r-bit counter, where r represents the resolution of the system. In this example, we’ll assume an 8-bit counter (range from 0 to 255), but the concept applies to counters of any bit width. The comparator is a simple circuit that compares the current count value from the counter with a predefined duty cycle value.
- Counter Operation: The up counter starts at 0 and increments by one with each clock cycle. When it reaches its maximum value (255 for an 8-bit counter), it rolls over to 0 and continues counting. This counting action forms the basis for generating the PWM signal.
- Duty Cycle: The duty cycle represents the percentage of time that the PWM signal is in the high state compared to the total time of one count cycle. In this design, the duty cycle is defined by a specific count value, let’s say 128.
- Comparator Operation: The comparator continuously compares the current count value from the counter with the duty cycle value. If the count value is less than the duty cycle value, the comparator asserts an output signal. Otherwise, it de-asserts the output signal.
- PWM Signal Generation: As the counter counts up, the comparator output remains asserted until the counter reaches the duty cycle value. Once the counter equals or exceeds the duty cycle value, the comparator output drops to zero for the remainder of the count cycle (up to 255). This behavior repeats with each count cycle, generating a PWM signal where the duty cycle determines the proportion of time the signal is high.
- Duty Cycle Calculation: To calculate the duty cycle, you divide the duty cycle count value (in this case, 127, as the count starts from 0) by the total count range (256 for an 8-bit counter). This gives you the percentage of time the PWM signal will be high during each count cycle. In this example, 127/256 represents the duty cycle of the PWM signal on the output.
Now Let us Design
It is really very simple
module timer_input
#(parameter BITS = 4)
(
input clk,
input reset_n,
input enable,
// output [BITS - 1:0] Q,
output done
);
reg [BITS - 1:0] Q_reg, Q_next;
always @(posedge clk or negedge reset_n) begin
if (~reset_n)
Q_reg <= 'b0;
else if (enable)
Q_reg <= Q_next;
else
Q_reg <= Q_reg;
end
endmoduleSo, above is a design of a up counter
- The counter is asynchronously reset to zero when the
reset_nsignal is active low. - If the
enablesignal is asserted and the reset is inactive, the counter operates. It loads the next count value into the register on the rising edge of the clock. - If the
enablesignal is not asserted, the counter remains in its current state without any changes.
Next state logic
assign done = (Q_reg == FINAL_VALUE);
always @(*) begin
Q_next = done ? 'b0 : Q_reg + 1;
endNow how do we calculate Duty cycle
The circuit generates a PWM signal based on the duty cycle value. To compute the duty cycle, you can follow this approach: the PWM signal remains ‘on’ from 0 to (duty – 1), where duty is the desired duty cycle. For example, if the duty cycle is set to 128, the PWM signal stays ‘on’ from 0 to 127.
The duty cycle of the PWM signal can be calculated as (duty – 1) divided by 2 to the power of r, where r is the bit width of the counter. For instance, if you have an 8-bit counter (r = 8), the formula becomes (duty – 1) divided by 256.
You can adjust the duty cycle according to your requirements by computing the appropriate duty value based on the desired percentage. For example, if you need a duty cycle of 50%, you can calculate the duty value as 0.5 * 256 = 128.
Testbench Design
The test bench for the pulse width modulation (PWM) signal involves defining signals, instantiating the unit under test (UUT), generating a clock signal, and manipulating the duty cycle to observe the PWM output. It follows these steps:
- Signal Definition: Define signals such as clock, reset, duty cycle, and PWM output.
- UUT Instantiation: Instantiate the PWM signal generator module within the test bench.
- Clock Generation: Generate a clock signal to drive the UUT.
- Reset Initialization: Initially assert the reset signal to initialize the UUT.
- Duty Cycle Variation: Change the duty cycle multiple times during simulation to observe different PWM output patterns, such as 25%, 50%, and 75%.
- Observation: Monitor the PWM output signal and verify its behavior for each duty cycle value.
module pwm_basic_tb (
);
localparam R = 8;
reg clk, reset_n;
reg [R - 1:0] duty;
wire pwm_out;
// Instantiate module under test
pwm_basic #(.R(R)) uut (
.clk(clk),
.reset_n(reset_n),
.duty(duty),
.pwm_out(pwm_out)
);
// Timer
initial
#(7 * 2**R * T) $stop;
// Generate stimuli
// Generating a clk signal
localparam T = 10;
always begin
clk = 1'b0;
#(T / 2);
clk = 1'b1;
#(T / 2);
end
initial begin
// Issue a quick reset for 2 ns
reset_n = 1'b0;
#2;
reset_n = 1'b1;
duty = 0.25 * (2**R);
repeat(2 * 2**R) @(negedge clk);
duty = 0.50 * (2**R);
repeat(2 * 2**R) @(negedge clk);
duty = 0.75 * (2**R);
end
endmodule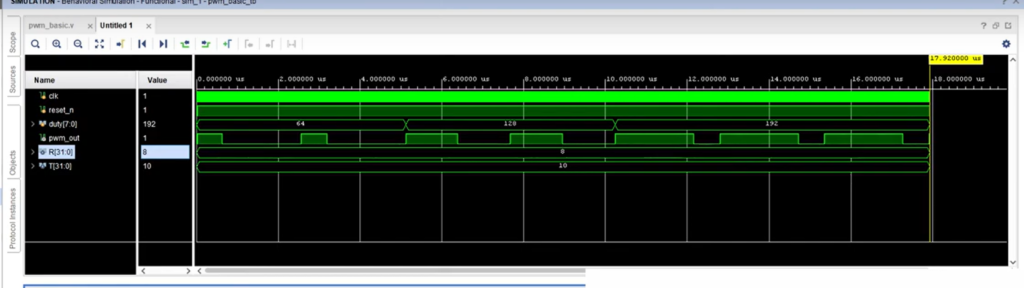
Design Issues
The counter in the design is an up counter that counts from 0 to 2^r−1, where r represents the number of bits in the counter. For example, in an 8-bit counter, r=8, and the counter counts from 0 to 255.
If the duty cycle value is set to the maximum value allowed by the counter, which is 2^r−1, the counter will count from 0 to the maximum value and then wrap around to 0 again. This results in an incorrect duty cycle calculation because the comparison with the maximum value is not exact due to the wrap-around behavior.
For instance, if the duty cycle is set to 255 (in an 8-bit counter), the counter will count from 0 to 254, and then when it reaches 255, it wraps around to 0 instead of staying at 255. This discrepancy affects the accuracy of the duty cycle calculation.
So to solve these issues we will see the improved design on Day 2
The sheer measurement of the bodybuilders fuelled prominence of
the game. The power displayed by athletes in the
weightlifting category, as properly as their physique, cultivated a culture of bodybuilding amongst
non-athletes. Steroid use would then become the drug many preferred of their quest to realize muscle mass.
Steroid does have makes use of apart from that of accelerating
efficiency.
These unwanted effects may go away during treatment as your body adjusts to the performance enhancing
drugs in the military (http://www.opencart-france.com).
Also, your well being care professional may find a way
to inform you about ways to stop or cut back some of these unwanted aspect effects.
However additionally they may relieve the inflammation, ache and discomfort of
many various illnesses and situations.
And most individuals taking prednisone are taking 10, 20 or maybe
a hundred occasions more than your body’s naturally occurring prednisone, cortisol.
So you are 10 or 20 or 100 instances inflicting
the unwanted side effects in your physique. Cortisol is often released in instances of extreme stress, it’s our stress hormone.
It helps us cope with disasters, whether it’s a famine or a war.
Cortisol was strategically created by Mom Nature to help us deal with those horrible times and isn’t worried concerning the future, it’s worried about
proper now, survival. That is it–it’s not holding back in any respect; it’s giving your physique every reserve
it may possibly discover.
Testosterone propionate is another fast-acting ester, albeit slower than suspension. Some bodybuilders view propionate as cost-effective because its value is decrease; nevertheless,
propionate is dosed at a hundred mg/mL instead
of the usual testosterone dosage, 250 mg/mL. Thus, users
pays 2.5 times the usual value to run a standard
testosterone cycle. Steroids can be included in a bulking stack to
accelerate muscle growth. When 4 steroids are taken at once, their effects mix to rapidly enhance bulky muscle mass.
It is a Steroid people will use to extend lean muscle mass and usually not be utilized
in a fats loss section. It does convert into Estrogen readily
and can trigger various bloating, making it better for bulking.
The dose of prednisolone you’ll take is dependent upon your well being drawback and whether you are taking it as a brief course or
for longer. An assistive gadget similar to a cane, crutch,
or walker can even help restrict pressure on the hip and cut back pain levels.
The type of remedy a person receives for hip pain will depend upon its trigger and severity.
The reviewers also suggest ordering repeat radiographs to check for joint modifications before additional corticosteroid injections.
This involves gradually reducing the dose over time to permit your body to regulate and keep away from withdrawal signs.
Once More, this process is critical for muscle progress and stopping muscle loss during cutting cycles.
This means you aren’t tied to the properties of only a single type
of testosterone. Sustanon 250 protects lean muscle tissue, and
your dosage and exercises will decide how a lot you’ll find a way to gain. One distinction many customers
discover is that NPP is slightly weaker in its actions, together with the good and dangerous
results. So usually, there are fewer gains and power and lowered water weight and suppression. A bonus is joint help; for
a few of us, that is the principle purpose to add NPP to the cycle.
Human chorionic gonadotropin (hCG) and Clomid are often adequate to get well endogenous testosterone
manufacturing, usually within 1–2 months. Failing
to manage PCT may result in users experiencing low testosterone symptoms
for several months. Testosterone and Dianabol are
each estrogenic and wet compounds; thus, gynecomastia should be categorised as high-risk.
To stop this, an efficient SERM can be taken, such as Nolvadex,
all through the whole cycle. Based Mostly on our exams,
we think about testosterone to have the most optimal safety
profile in comparability with different anabolic steroids.
If you measure your blood strain and the highest number (systolic) is one hundred eighty mm Hg or larger or the
bottom quantity (diastolic) is a hundred and
twenty mm Hg or greater, get medical attention immediately.
Will Increase in blood pressure is probably not
noticeable, but look out for and tell your healthcare provider immediately if you
have any of the following symptoms of severely high blood
pressure. Speak to your healthcare provider about tips on how to keep wholesome blood
sugar levels. Maintain all appointments with your healthcare supplier to check your blood work.
Name your healthcare provider if you have the following signs of high blood
sugar. Long-term use of prednisone could trigger your body’s adrenal glands
to stop making as a lot cortisol (the stress hormone).
But let me let you know, D-Bal Max stands head and shoulders above the rest.
It’s not just one other overhyped product; it is the closest legal alternative to Dianabol I’ve ever come across.
Licensed pharmaceutical retailers are a highly dependable and respected option for acquiring Stanozolol within the USA.
Not all merchandise are created equal, and a few make daring claims with
little scientific backing. Use this guide that can assist you select a safe, efficient, and respected legal steroid that aligns
with your objectives. Chemically, the potent anabolic (muscle-building) and lipolytic (fat-burning) effects of anabolic
deca steroids reviews (Nelly) are as
a outcome of them both being exogenous forms of testosterone.
The merchandise talked about are described as safer alternate options to anabolic steroids, with fewer unwanted effects.
However, it’s at all times emphasised that they should be used responsibly and
along side correct coaching and diet. Now, I at all times stress to my shoppers that no
complement is with out dangers, and Testol one hundred
forty is not any exception. Nevertheless, compared to conventional anabolic
steroids, the aspect impact profile is far milder.
If you could have a prescription for anabolic steroids,
you might also use licensed online pharmacies to purchase your treatment.
It is necessary to confirm that the web pharmacy is reliable
and controlled. Look for accreditation from organizations just like the National Affiliation of
Boards of Pharmacy (NABP) and check that the pharmacy requires a prescription. Use of medicine merchandise marketed with
unproven claims or containing hidden drug ingredients may cause severe well being issues.
FDA urges consumers to stay knowledgeable, know the
risks, and prioritize your safety. Some of the medicine were even of similar composition to sure FDA-approved medicine that require particular
boxed warnings on their labels to emphasise serious
potential unwanted side effects, including pulmonary embolism.
When Health Canada identifies unauthorized products which will pose critical well being risks, Well Being Canada takes acceptable motion and informs Canadians.
This contains seizing unauthorized merchandise and dealing with
the Canada Border Providers Company (CBSA) to assist stop further importation of unauthorized merchandise.
Every of those dietary supplements has been extensively researched and examined
to guarantee that they are protected and efficient for customers.
Pretend or low-quality steroids could be dangerous and should cause severe well being
problems. Look for suppliers who supply their products from
reputable producers and who provide detailed information on the merchandise they’re selling.
It is not illegal to own HGH in Canada for personal
use, however it’s a controlled substance and requires a prescription from a doctor.
Steroids are labeled as managed substances in Canada and are illegal to own. If you may be contemplating utilizing anabolic
steroids as a Canadian or somebody living in Canada, then this text will be of great interest to you.
Thus, with restricted analysis, we have no idea whether or not turkesterone can produce steroid-like results in natural bodybuilders.
Turkesterone may be extracted by way of pure means; thus,
it’s suitable for pure bodybuilders. It can be 100% authorized to purchase and has not been banned by
any sporting federation.
While irritating, we are ready to assure you the anabolic steroid market is really vast,
and whereas it is plagued with horrible suppliers there are more
than enough high quality steroids to go round.
Do your homework, search out as many suppliers as you’ll find a way to, and
when you find them make positive you analysis their data out completely.
Via a search, it is possible for you to to find out if
your proposed provider is value his salt or if he must be ignored;
once more, this can take persistence, however what’s worse, being affected person or losing your money on trash?
If we now have to reply this question, you have greater problems than we might help you with.
His fraud extended to posting misleading Certificates of Evaluation on the Rat’s Military website to
convince customers that the merchandise have been respectable and
protected to devour. All of these legal steroids are backed
by 100%-money again guarantees, so you possibly can order in confidence and check them with out risking
your cash. The research reveals that it could considerably enhance testosterone ranges
by 44% or more, which is essential for muscle progress.
Suma root is usually called “nature’s anabolic steroid” and has a
confirmed capability to extend protein synthesis and muscle
development. We have treated people who have taken as a lot as 10–100 instances the really helpful therapeutic dosage.
The addictiveness of anabolic steroids is seldom spoken about, yet it remains one of the largest issues for our doctors right now.
It is at all times a problem to get sufferers off anabolic steroids long-term
when their brains have turn out to be accustomed to exceptional surges in dopamine on-cycle.
At a extremely competitive price, it’s one of the most accessible choices for anyone seeking to bulk up quick.
You can grab it instantly from trusted retailers on-line, making
it a hassle-free selection for remodeling your
physique. What we also like about Dbal is its versatility—it works well by itself,
nevertheless it may additionally be stacked with different dietary
supplements to amplify your outcomes. Plus, it’s simple to include
into your routine, whether or not you’re hitting
the fitness center exhausting or simply starting a
new bulking phase. Last, 75% of web sites supplied suggestions
for specific product stacking and cycling regimens.
Many of these sites contained unmonitored blogs or evaluate columns permitting for detailed info and buyer suggestions
on the use of every product.
Biggest Physiques is the number one vacation spot for
the best wanting our bodies on the planet. We cover
skilled athletes, models and even social media stars to convey you the
easiest, updated info in our profiles. My lady has been trying to comply with her lead and can’t eat all that.
After slowly increasing the weights on the bar by 5 lbs or 10 lbs, after 1 yr
of figuring out in the fitness center, Cass lastly began to see results.
After attending a Mr Olympia show with her boyfriend, Hunter
Martin, Cass had made her decision to dedicate time to sculpting a powerful physique.
Cass Martin grew to become intrigued with fitness after seeing one of the early feminine
icons, Jamie Eason, on the duvet of magazines in shops.
I agree, she must be taking much more than simply pre exercise
and protein, however okay. Cass goals to eat as a lot as 6 meals per day, keeping her physique fueled, and her metabolism
excessive. While cutting body fat, she eats very clear, maintaining her carbs to a minimal.
Through exhausting work, determination, and the assistance of her fitness-obsessed boyfriend,
Cass made serious progress to her figure. This page may include sensitive or adult
content that’s not for everyone. To view it, please log in to verify your age.By continuing, you additionally agree that use of this site
constitutes acceptance of Reddit’s User Settlement and
acknowledgement of our Privateness Policy. While there have been others
corresponding to Rachel McLish and Jamie Eason that have
hit the spotlight, Cass Martin has gained online consideration like no-one else before her.
At first, the video had no exposure as she had no followers.
Her boyfriend was an enormous fan of bodybuilding and
had been lifting weights for a number of years; he offered
the mandatory motivation to push Cass Martin into the fitness center.
It also helped that she knew some IFBB Professionals and
knew that weightlifting was the necessary thing to unlocking
the determine she wanted. Cassandra Martin is
very in style in comparison with other fitness models, which makes her the first choice when it comes to brand promotions and commercials
for supplement manufacturers.
Cass Martin’s exhausting work out and healthy diet reveals how a lot health craze and thirst is there in her.
Her recognition is increasing daily via his followers which leads
and encourages different women to build heavy builder bodies like her.
Cass Martin works out 6 days per week with heavyweight and she’s going to mix her workouts so her physique doesn’t get
used to a certain routine. Due to her ardour for bodybuilding, Cass is now admired on bodybuilding boards
all over the internet. This is simply one of the locations where she inspires an enormous fan-base to start their health journey, and to
lead a healthy lifestyle of their own.
Cass Martin is an American fitness mannequin and social media sensation. Her actual
name is Cassandra Martin, however she is properly acknowledged by her
nickname, Cass. She is one meaning of steroids the hottest female health
models on the earth.
Collectively, they continue to inspire others with their health journeys and
serve as a testomony to the significance of having
a supportive and loving partner by one’s facet. Nonetheless, A mesmerized welcome was given to her by
followers, she began to realize recognition over a short time period and getting daily new followers.
Everyone was loving her muscular and highly effective physique and that too being a lady.
Cass enjoys training 6 days per week with heavy weights, always pushing her
limits. She’ll mix up her exercises so her physique doesn’t get used to a sure
routine – sometimes performing 3-7 reps in sets
of 4, however then performing up to reps in other classes.
At the age of 23 years, Cass started her health journey and used to go to the
gym. She was very impressed by Dana Linn Bailey, and
after a few months within the gym, she began heavy weight lifting.
Welcome to probably the most lively subreddit for followers of The Final of Us.
(The SECOND The Last of Us sub, the 2 doesn’t stand for Part 2)Criticism is allowed.
Cass trains particular person muscle teams every day, aside from leg days,
as she believes her body responds the most effective to this.
She works by way of four exercises per session, adding in super-sets often. Cass
had at all times been aware of the fitness industry as a end result of her
partner’s keen curiosity in it. However, she solely discovered the need to sculpt her dream physique after seeing feminine bodybuilding icon, Jamie Eason, on the quilt of a journal.
Apart from that, Cass Martin actually hasn’t given much away about her diet.
However in a few of her videos, she could be seen figuring out together with her husband.
Cass often goes for heavy weights and excessive reps during her workout
and loves workouts such because the deadlift, again squats,
and bench presses. She’s additionally fond of old-school workout routines, like one-arm rows, massive three, and
T-bar rows. Cass Martin always takes care of her diet and eats healthy only.
She takes 6 meals in a day to maintain her physique strong and stamina excessive.
Though, Cass Martin has already determined her diet and she or he
runs based on it consuming recent green vegetables and carbs.
At the tip of 2016, Cass had a sea of followers which she hadn’t
imagined.
Keep reading to be taught more about what
forms of medicine are prohibited in Florida, the place they
fall beneath the scheduling classification, and the severity of possessing these drugs.
Unsafe on-line pharmacies supply potentially dangerous prescription drugs to U.S.
consumers. FDA has issued warning letters informing the internet site operators they’re engaged in criminal activity in violation of federal regulation. Even in worldwide locations the place
it’s authorized to use marijuana recreationally, importation restrictions could exist, or definitive steerage may be unclear.
Players are ordered by the introduced date of their suspension, placed in the appropriate table
per their MLB expertise and roster status at the time they were suspended.
Players who are lively in skilled baseball (not restricted to MLB) are listed
in italics; gamers who’ve retired or have been a free agent for over a 12 months aren’t considered “active”.
Such collaboration is a powerful deterrent to those attempting to engage in illicit activities on-line.
The finest legal steroids are made with pure ingredients like herbal extracts and vitamins,
and there are many on this listing to select from.
Think About a pure anabolic steroid that comes with a clear
list of elements, so you realize exactly what you’re putting in your physique as you’re employed to gain higher muscle.
Though legal steroids will not be as robust as medical-strength steroids, they’re much safer and may nonetheless ship
thrilling advantages for muscle power and fitness
center targets. The closest factor to authorized steroids is natural steroid alternate options produced from potent herbs and nutrients.
Big Nutrition Rebirth PCT is the best post-cycle legal steroid that reduces estrogen, promotes lean mass gains, and encourages wholesome testosterone ranges.
Supportive remedies and medicine interventions
could also be wanted for extreme habit. Medications which were used for
treating anabolic steroid withdrawal permit the pure hormonal system to revive.
Kacper Fratczak, competing in the sport of Kickboxing,has been suspended after testing positive on the prohibited substanceViolation of the
Prohibition of Participation During Ineligibility. In drugs,
this treatment has been categorized as a androgenic hormones.
Johaug received a 13-month ban for testing positive, costing her the 2018 Winter Games in PyeongChang, South Korea.
Additionally, folks that identify themselves other than males
should also not use these products and make contact with healthcare suppliers to understand the role of legal steroids.
At the 1998 Winter Olympics in Nagano, Canadian snowboarder Ross Rebagliati won a gold medal in big slalom.
Rebagliati subsequently examined positive for marijuana, after which a sequence of Olympic boards voted to strip him of
the medal. An appeal to the Court of Arbitration for Sport was shortly rewarded,
and Rebagliati was capable of hold his medal. Whereas a
few of these unlawful steroids are safer than others,
all of them could cause you to experience unwanted side effects.
You might even spend a while in jail if you are found
in possession of those managed substances with
no prescription. The use of performance-enhancing substances or methods to
enhance an athlete’s capability to succeed in competitive sports is a pertinent and well timed topic for athletes,
coaches, and any concerned well being care supplier.
In addition, the report names 89 MLB gamers who are alleged to have used steroids or different performance-enhancing medication. Modern sports activities
typically require athletes to bear drug testing for quite a lot of substances.
Everything from human growth hormones and steroids to performance-enhancing medication and
different stimulants can give athletes the edge they need to win. Of course, it is also thought
of dishonest and can price an athlete their medals, titles,
and profession. Doping, in a single type or one other, is nothing new
– athletes have been utilizing substances to boost their skills for tons
of of years. The anabolic steroids lined on this article — together
with testosterone enanthate, trenbolone, Winstrol, Deca-Durabolin, and others — are classified as Schedule III
managed substances beneath the us
This substance was first listed in the IOC doping record on 31 January 1998 as a stimulant and beta-2 agonist.
Zeranol is listed under anabolic agents within the
WADA Prohibited Substances Record. It is a mycotoxin, derived from fungi
within the Fusarium family, and could also be found
as a contaminant in fungus-infected crops. In the US studies has proven that beef cattle are given this steroid to make
them fatter faster, to save cash. This anabolic steroid was first referenced in WADA-related documents in 2004.
This substance was first listed in the IOC doping list on 31 January 1998 as
an anabolic agent.
They can also enhance performance, pace up restoration,
and improve appetite. Make certain that you are doing so within the law and
that you’re totally aware of the potential penalties.
I even have notes from the Winter Meetings where the house owners group and the gamers’ affiliation sat in meetings with the team physicians
and team trainers. And team physicians stood up and mentioned, “Look, we need reasons to take Steroids do one thing about this.
We’ve received a problem right here if we don’t do one thing about
it.” That was in 1988.
Armstrong additionally won a bronze medal at the 2000 Olympic Games and was a celebrity in and outdoors the game. His name invoked athletic superiority and beating the chances, nevertheless it all came crashing down in 2009 after bicycle owner Floyd Landis admitted to doping and alleged the same for Armstrong. In 2013, Braun’s name appeared a number of instances within the Biogenesis scandal, leading to a nice deal of scorn and a 65-game suspension. Many of Braun’s peers branded him a as a liar and vilified the left fielder for some time. Finally, Braun admitted to utilizing PEDs, calling it a mistake and acknowledging that he compounded the state of affairs by denying his use of PEDs. Moreover, Braun apologized to Dino Laurenzi Jr., the urine test collector he accused of mishandling his pattern in 2011.
Anabolic steroids, medically often identified as anabolic-androgenic steroids, are synthetic versions of the male intercourse hormone testosterone. They are sometimes prescribed to deal with hormonal conditions, like delayed puberty, or situations that lead to muscle loss, like most cancers or AIDS. Anabolic steroids are illegal within the US without a doctor’s prescription.[1] X Analysis supply Accordingly, you will need to analysis whether or not the person has authorized permission to use the steroids. Pay consideration to common signs someone is using steroids and notify appropriate officials of suspected steroid use. Anecdotal stories of the abuse of human growth hormone (hGH) by athletes have been circulating for a number of years, particularly since the early Eighties. Till recently, there has not been a reliable check out there to detect abuse among athletes.
Anabolic steroids are prescription drugs with medical uses together with the treatment of delayed puberty, losing circumstances, and osteoporosis. But they also could be illegally used without a prescription by bodybuilders and weightlifters, as properly as these competing in varied sports activities. Natural steroids are a lot safer than artificial formulas as a end result of they do not induce any side effects or put health in danger.
Oxandrolone doesn’t aromatize and there shall be no water retention, and
like all anabolic steroids it can’t promote fats gain. It’s true a person mustn’t expect large buildups
in size or weight as a outcome of this steroid’s use,
but the positive aspects shall be strong and infrequently easier to maintain submit use in comparability with some steroids.
The majority of the questions, concerns, and points where female use is worried will be
explored upon in a later article. Anabolic steroids are medicine that
resemble the chemical construction of the intercourse hormone
testosterone, which is made naturally by the physique.
Testosterone directs the body to make or improve male characteristics, similar to increased muscle mass, facial hair growth, and deepening of the
voice, and is a vital a part of male development throughout puberty.
While you’re utilizing the steroid, you won’t have
symptoms of low testosterone. Still, as quickly
as you cease taking Anavar, and where no different form
of exterior testosterone is being taken, you presumably can experience a sudden drop in T ranges
– particularly as Anavar leaves the physique
rapidly. A standard PCT cycle will often not
restore testosterone ranges following Trenbolone use, and longer-term TRT can be required.
Nonetheless, it isn’t doubtless to be used in pure bulking cycles as a end result of there’s a restrict
to only how high your dose of Anavar should be before
well being dangers kick in. Anabolic steroids have been round for many years,
athletes began using anabolic steroids in 1954 in the course of the Olympics.
Russian weight lifters were given doses of testosterone to help improve athletic performance.
So, while girls have low ranges of natural testosterone, even a small exogenous administration taken often goes to have an enormous effect!
That’s why females can quickly placed on lean muscle with
very low doses of anabolic steroids. It’s additionally
why those same low doses can shortly result in undesirable side effects developing44,
a lot of which are going to be very completely different from
the kinds of side effects that male steroid customers fear about.
Until absolutely necessary, such because the case of female aggressive bodybuilders, stacking
should be averted in any respect costs except deemed
completely needed. In such a case, it’s a personal determination primarily based upon private values and goals.
Nonetheless, for the typical female that doesn’t wish to transform right into a male, it’s advised to
avoid the robust androgens such as Testosterone.
Variations in anabolic steroid utilization protocols between female and male users.three.
Anabolic steroids thought of suitable and low-risk for
female anabolic steroid cycles.4.
It’s one of the costlier steroids, so if cash is tight, this may be one you’ll should skip in a long cycle.
To get the most effective from Primobolan,
you do have to take higher doses, and this, in fact, pushes the cost up
additional. In my experience, these cycles have their place, BUT you better have a good cause for eager to go in this direction as
a end result of it won’t be with out its downsides. As the
first male natural steroid hormone, unmodified testosterone steroids (synthetic types of the hormone)
are often the first place we start if utilizing steroids for the first time.
So if you’re utilizing an injectable steroid with a half-life of roughly eight days and take a 400mg dosage, at the 8-day
mark (or thereabouts), there shall be about 200mg of the steroid circulating
in your physique. Steroids have a strong anti-catabolic impact on muscle tissue (after
all, they are ANABOLIC steroids – the alternative of
catabolic). Stress hormones like cortisol, naturally rising throughout intense train, contribute to muscle breakdown and loss.
Nonetheless, most ladies will discover that Anavar is extra well-tolerated in terms of controlling the unwanted aspect effects.
For women who wish to use Winstrol, the oral type only is beneficial, and
doses must be stored very low to keep away from virilization. When Anavar is used at dosages that
meet the wants of bodybuilders, it does end
in suppression of the HPTA (Hypothalamic Pituitary Testicular Axis),
bringing about testosterone manufacturing suppression. The stage of that is
thought of quite excessive and, as anticipated, rises the higher your dosage of
the steroid is.
In other words, there are likely many adolescents who use alcohol or marijuana but no different drugs, lowering the affiliation between these
substances and AAS use. Use was larger among boys than ladies (3.46% vs.
2.41%), a discovering that’s according to earlier research (Bahrke
et al., 2000). Hispanic/Latino youth had the very best prevalence of AAS use, adopted by Black youth.
In brief, this methodology makes it each less painful and more convenient
to manage your injections. Since you should use new
sterile tools for each injection, you can undergo many objects in a long
cycle. Buying in bulk will prevent money and ensure you will not have to worry about working out and being tempted to
reuse items, risking your well being. 3ml or 3cc, or 5ml/5cc are
the most typical syringe sizes or capacities.
Syringes are low-cost items, and stocking up is simple, so you might have more than sufficient to final a very long time.
Nevertheless, dying by way of liver cirrhosis is feasible if Primobolan is taken in excessive
dosages for excessive periods or given to debilitated people.
Primobolan (methenolone) was first described in 1960 and was
utilized in medication to counteract the catabolic effects of long-term corticosteroid use.
Winstrol dosages above 5 mg are likely to trigger complications for ladies
looking to keep away from masculine traits.
Girls usually take 5–10 mg of Anavar with no issues; nonetheless, 25 mg of Anadrol is
(surprisingly) considered an excessive dose for women, but in fact, it is protected for sustaining femininity.
“5 mg of anavar is roughly the equal of 25mg of anadrol for threat of virilization”.
Heavy consumption will current much more stress to the liver and
greatly improve the potential for harm. Many over-the-counter drugs are quite hepatotoxic and ought to
be restricted to when solely completely needed.
The liver carries a variety of the most exceptional
rejuvenation traits of any organ within the body and
if proper steps are adopted and no underlying points
exist no damage ought to be done.
Prednisone is a steroid medicine that treats conditions like asthma, allergic reactions, arthritis,
inflammatory bowel illness and adrenal, blood or bone
marrow conditions. It decreases inflammation, slows an overactive immune system
or replaces cortisol. Cortisol is a hormone that helps your physique respond to stress, injury
and illness.
You might need a quantity of of those objectives, however ultimately, what you wish to achieve from your steroid cycle will determine what
you’re taking and how you are taking them. Biking
requires a plan19, as you’ll decide how lengthy you wish
to take the steroid and the way long the break in between will
be whenever you cease utilizing it. A cycle
can range wherever from a quantity of weeks up to several months of usage, followed by a
interval with either no steroid use at all or utilizing at
a lower dosage. Your cycle size will depend on your experience with steroids,
which steroid you’re taking, and what objectives you’re attempting to
realize. In actuality, both oral and injectable steroids include their own set of risks, and it’s up to YOU to weigh
up the risks versus the rewards earlier than deciding on what kind of steroids
(if any) you’re going to be comfy utilizing. Whether Or Not you need to appear to
be the Arnie of yesteryear or need to get your body into peak conditioning with
the most ripped physique you possibly can muster, we know
that many people do it with an educated use of steroids.
When it involves bodybuilding and athletic efficiency,
we primarily talk about steroids in the form of anabolic-androgenic Buying
Online Steroids – http://Jointjedraaien.Nl/Images/Pages/?Anavar_Kopen_1.Html –
(AAS)3.
This usually ends in a person in search of help again for poison ivy.
Dealing with pain as a result of a chronic inflammatory illness may be
challenging, and it can be tough to search out the proper
way to cope with it. You do not want to attempt this alone; your healthcare supplier
will assist you to develop a long-term ache management therapy.
However, whether it is virtually time on your subsequent dose,
skip the missed dose and go back to your regular dosing schedule.
Do not take extra of it, don’t take it extra often, and do not take it
for an extended time than your doctor ordered. All The Time
consult your healthcare provider to make sure the information displayed on this page applies to your personal circumstances.
Dupixent is used to treat eczema, eosinophilic or oral-corticosteroid-dependent asthma, persistent …
Long-term use of steroids could result in bone loss (osteoporosis),
especially when you smoke, if you don’t exercise, if you don’t get enough vitamin D
or calcium in your food regimen, or in case you have a household history of
osteoporosis. Name your doctor without delay if you have shortness of
breath, severe pain in your upper stomach, bloody or tarry stools, extreme despair, adjustments
in persona or behavior, imaginative and prescient issues, or eye
pain. Prednisone treats many alternative
circumstances such as allergic problems, skin conditions, ulcerative colitis, arthritis,
lupus, psoriasis, or breathing problems.
In giant doses, prednisone could cause your physique to retain salt or
lose potassium. Your physician might recommend changes to your food
plan to manage this facet effect. The actual price you’ll pay depends on your
insurance plan, your location, and the pharmacy you
utilize. Earlier Than taking prednisone, talk along with your doctor and pharmacist.
Inform them about all prescription, over-the-counter, and other
medicine you are taking. Additionally inform them about any nutritional
vitamins, herbs, and supplements you employ. Sharing this data might help you keep
away from potential interactions.
The review acknowledged that it fulfils the PRISMA checklist (Moher 2009); nonetheless,
reporting of the information collection process and knowledge items had been unclear and no meta‐analysis was tried (Suresh 2016).
The out there evidence suggests that topical corticosteroids
may be efficient for treating painful oral lichen planus, however our confidence in these findings is limited as there were solely a small number of research and participants.
There is some evidence that tacrolimus could additionally be simpler than a corticosteroid, but evidence on negative unwanted effects is inconclusive.
Steroid injections, typically called cortisone photographs, are injections of artificial medication called corticosteroids
that may assist ease ache and inflammation (swelling) in specific areas of your body.
Corticosteroids are similar to cortisol, a hormone your physique makes in your adrenal glands.
They are not the identical because the hormone-related steroid compounds that some athletes use.
Oral Turinabol is suppressive to natural
testosterone and ought to be used at the side of exogenous testosterone.
As you’ll quickly discover about Primobolan (and one thing
I like to mention regularly), this is recognized as a very protected AAS.
So a lot in order that it has been used efficiently and without problems in youngsters
and premature babies to advertise weight acquire.
Physician reported oral corticosteroid dosage and
treatment patterns. Your physician will advise you on the proper dose, which is dependent upon your situation and your weight.
If you’ve been taking steroids for an extended time, your doctor will make any reductions very slowly.
Whereas less frequent, probably the most severe unwanted
facet effects of prednisone are described beneath,
along with what to do in the event that they happen. Prednisone
must be stored at room temperature, between 68 F to
77 F (20 C to 25 C). It may be uncovered to temperatures between 59 F to 86 F
(15 C to 30 C) for shorter intervals of time, similar to when transporting it.
The concentrated resolution must be thrown away 90 days after the bottle
has been opened. If you miss a dose of this drugs, take it as quickly as attainable.
Herein, Lp(a) plummeted (-83%) compared with
baseline after 8 weeks, with partial return to baseline 6 weeks after cessation of AAS use.
Finally, in the HAARLEM examine Lp(a) decreased by nearly 50% at the end of an AAS cycle and returned to
baseline 3 months after cessation of use (46). Therefore, it
shouldn’t be assumed that an AAS-induced decrease in Lp(a) might
negate the other results that are detrimental to cardiovascular well being.
The Boldenone hormone does not aromatize closely, but it is aromatized to estrogen nonetheless.
This is because of the testosterone hormone’s interplay with
the aromatase enzyme.
AASs travel via the bloodstream to the muscle tissue, the place they bind
to an androgen receptor. The drug can subsequently work together with the cell’s DNA and stimulate the protein synthesis course of that
promotes cell development. There are as a lot as 32 forms of anabolic steroids listed on industrial websites.
In uncommon instances, long-short term effects of anabolic steroids use of high doses
of corticosteroids may cause permanent bone damage called osteonecrosis or aseptic necrosis of
the bone. If you’re apprehensive about side effects
or they are bothering you, speak to your
healthcare provider.
Since the medicines may contribute to osteoporosis, your physician might advise
you to increase your vitamin D and calcium intake or start taking
medications to battle bone loss. Oral steroids come in tablet or capsule type,
making them convenient and simple to make use of. However,
they are metabolized by the liver, which can result in strain on this organ if not used responsibly.
If people are thinking about pure steroid dietary supplements, the safest choice is to
consult with a physician earlier than taking any dietary dietary supplements.
For example, testosterone deficiency is rare in males under age 50.
While gynecomastia can develop in patients with hyperprolactinemia, the situation arises secondary to the gonadotropin suppression prolactin may
cause (203). Such apply ought to be discouraged because it is illogical and produces possible side effects similar to cardiac abnormalities or arrhythmia.
Elevated progestin motion on the mammary gland can be very unlikely to be a reason for AAS-induced gynecomastia.
AAS do not enhance progesterone ranges and solely a choose
few show significant progesterone receptor activation (205).
Moreover, no gynecomastia was famous in a 6-month
hormonal male contraception examine combining administration of testosterone enanthate with
the potent progestin levonorgestrel (0.5 mg daily) (183).
A few reports in the literature have linked AAS use to focal segmental glomerulosclerosis (FSGS) (169–171).
FSGS is a histopathological finding marked by glomerular lesions,
mediated by diverse insults directed to, or inherent inside,
the podocytes (172).
Regardless, persistent AAS-induced hypogonadism has been reported within the literature in a quantity of
cases (65, 178). Future research is required to delineate the
AAS cycle options or affected person characteristics that hinder restoration and end in partially reversed, extended, or persistent hypogonadism.
A trial in older hypogonadal males randomized to TRT
with or with out the 5α-reductase inhibitor dutasteride famous
no change in CEC (137). CEC also remained unchanged in transgender males (female to male) present process treatment with testosterone gel or injections (138).
In distinction, cross-sectional analysis demonstrated impaired CEC in AAS
customers compared with age-matched, strength-trained nonusers and
sedentary controls (139). It is feasible that the higher dosages
used, use of varied AAS, or completely different
strategies used to measure CEC (which just isn’t standardized), would possibly underlie these variations.
The detrimental results of these seemingly small increases in blood
stress shouldn’t be underestimated.
Steroids have been proven to have a constructive impression on these features of athletic efficiency, enabling athletes
to push themselves harder and perform at a higher level for prolonged durations.
Anavar can also be utilized by experienced steroid users when chopping to maximise fats loss whereas retaining muscle
tissue. Our liver function checks present Winstrol
to be hepatotoxic; thus, customers usually take a liver help
supplement (such as TUDCA) to forestall liver enzymes from rising to excessive
ranges. Winstrol’s power lies in its low affinity to bind to SHBG (sex hormone-binding globulin), releasing up more energetic testosterone that is utilized for triggering lipolysis and will increase in skeletal muscle.
We have had success with sufferers taking cabergoline alongside Deca Durabolin, which is actually a supplement to inhibit prolactin production. This allows bodybuilders to cycle Deca and keep
their sexual health. We find that testosterone is often the first steroid a bodybuilder
will take because of its mild nature and safety (in terms of
side effects).
In uncommon instances, some folks have had liver tumors or blood-filled cysts within the liver and/or spleen. Name your health care provider instantly if you have
any of the following signs of liver harm.
As Quickly As using Deca Durabolin has come to an end
and all the exogenous steroidal hormones have cleared your system, natural testosterone
production will begin again. It won’t happen in a single
day, and because of this a Submit Cycle Therapy (PCT) plan is usually really helpful.
This will velocity up the recovery course of
in addition to enhance the general effectivity. No,
contrary to in style myth, there is no PCT plan that may return your natural testosterone ranges back
to regular all on its own. Nonetheless, a PCT plan will ensure you’ve enough testosterone in order for proper operate while your
levels proceed to naturally rise.
Oral steroids can even lead to liver bother,
together with the event of tumors, in accordance with research printed in Could 2020 in LiverTox.
These are all positive attributes to supplemental or exogenous testosterone use and
the identical results can be achieved whatever the
form of testosterone we use. While these are not the one optimistic traits these are the most elementary to our process and important to our targets
revolving round testosterone use.
Due to its large therapeutic benefits, the Nandrolone hormone is probably considered one of the most beneficial anabolic steroids
in medical apply. Nevertheless, as a end result
of years of anabolic steroid controversy such use has
been fairly limited in the U.S. for a few years.
Deca Durabolin remains a bit more popular in therapeutic remedy plans that can cover a number of areas.
In contrast with the opposed impact on LDL- and HDL-cholesterol, AAS appear to exert a impartial or
favorable impact on lipoprotein (a) (Lp(a)).
LH gets the testes to make testosterone, so HCG might help get the testosterone production started once
more. Also, using anabolic steroids can mess up the body’s natural manufacturing of hormones,
leading to a hormone imbalance. PCT is a process designed to help the body get its hormones again in steadiness after utilizing steroids.
Water retention and swelling are unwanted aspect effects many
anabolic Steroids description steroid customers might be familiar with.
The wrists and ankles are mostly affected by water retention, leading to a noticeable swelling of those areas,
which may hamper your motion.
Nonetheless, many individuals will find that a lower dose provides substantial benefits whereas decreasing undesirable facet effect dangers.
This dose can be Ostarine at 15mg daily and Cardarine at 10mg
daily. Cardarine will make your physique use fats as gasoline, leading to potentially very quick
fat-burning quickly after beginning this cycle.
You can’t assume one 12 months to the following that the same avoidance strategies
will work. Some current advancements in anti-doping testing that labs have developed embrace gene
doping exams, retroactive liquid testing, and long-term metabolites.
It can generally take a few months after stopping your PED cycle earlier than your regular menstrual cycle resumes.
Some ladies will find a quick restoration of regular cycles; this will depend on the individual
and which PEDs were taken. Steroids which have more powerful androgenic properties would be the steroids that can cause virilization faster and extra severely than steroids that have a lower
androgenic rating.
This isn’t a steroid that’s going to have you ever
putting on huge mass in a single day, however
steady quality positive aspects are what you’ll be able to look forward to.
Stacked with a moderate dose of testosterone, positive aspects of 10-15lbs of quality size is
a reasonable goal, with new customers able to goal for
25lbs. Of course, efficiency use just isn’t the meant objective of Deca-Durabolin, and medical
doses would rarely match these used by bodybuilders.
PCT or Publish Cycle Therapy is a restoration part throughout which your body’s endogenous hormonal
production is restarted. PCT is often utilized when folks
do steroid blasts for brief intervals of time. If you’re cruising
on testosterone endlessly, then the knowledge in this
article does not apply to you. You won’t discover any pharmaceutical-grade Ostarine for sale anywhere
because this SARM (as with all SARMs) has no approval for medical use.
It’s still being researched and investigated for potential
future medical purposes, but there is no guarantee that it’s going to ever happen. Subsequently, the closest you might
get to the pharmaceutical grade when buying Ostarine is to get a research grade.
This additionally supplies a legal loophole that athletes and bodybuilders have lengthy
taken advantage of.
Post-cycle remedy (PCT) is a protocol used to restore
the user’s natural testosterone production after a cycle of anabolic steroids like
Primobolan (methenolone enanthate). Clomid (clomiphene citrate) is commonly
prescribed as a half of PCT to stimulate the body’s natural hormonal operate.
PCT can also embody testosterone enanthate to assist
keep regular testosterone ranges till the body can resume its natural manufacturing.
One of the most important advantages of PCT is the retention of muscle mass gained
in the course of the steroid cycle. Without PCT, people typically experience
muscle loss because of the sudden drop in testosterone ranges.
You might not have gained a lot mass, but your physique will still look considerably more muscular – no water retention, either.
Intermediate customers shall be at the stage
where you’re snug stacking Clen with a minimum of
one different compound. Nonetheless, the general goal shall
be a cutting cycle where fast and powerful fat loss is a precedence, as is retaining lean muscle and achieving a toned
and ripped physique. The period of a steroid cycle is a crucial factor in attaining optimal outcomes while minimizing dangers.
Steroids have a big influence on our organism, and people
who discover themselves taking them shouldn’t stop using them abruptly.
Though women have a fraction of the testosterone in comparability with men, it stays an essential hormone
of their body chemistry. Excessive doses of Anavar give me again pumps and jaw pumps as if I am chewing
robust meat like beef jerky. I never do over 40 mg
on orals as a outcome of back pumps are annoying,
and by no means more than 4 weeks. The Anavar dose under reflects a cautious dose utilized by our feminine sufferers.
A higher dose of Anavar is more frequent among more skilled users, commencing
at 10 mg per day.
HGH (Human Development Hormone), Clenbuterol (Clen)
or Cytomel (T3) are medications that added to a chopping stack improve the
potential of fat loss steroids and make you try and do away with fat an actual success.
To truly unlock the total advantages of these highly effective
muscle-building formulation, you need the
best technique. Here’s how to guarantee you get sooner, higher, and longer-lasting outcomes out
of your legal steroid cycles. Top legal steroid companies usually offer
bundle offers, multi-buy reductions, and even free world transport.
If you’re considering of utilizing steroids, do not panic as they are often very extraordinarily helpful in sure
situations. Apart from drastic fats loss and an improvement in muscle tone, users report energy gains nearly instantly.
Your first exercise whereas utilizing Winsdrol, you’ll notice an enchancment in power and muscle endurance.
what Is the safest anabolic steroid this implies is that Winsdrol not solely burns fats at an accelerated
rate but also allows customers to add lean muscle mass in very brief time frame.
The Designer Anabolic Steroid Management Act of 2014 banned many
anabolic dietary supplements, androgenic steroids, and methylated
prohormones. The excellent news is that there are still many approved legal-steroids & fat burners
nonetheless out there to make use of. Moreover, combining oral anabolic
steroids with prescribed hepatotoxic drugs may cause liver issues.
With near-perfect rankings, Osgear continues to uphold its popularity as a trusted and
high-performing on-line retailer for steroid merchandise. Extra sugar can lead to insulin resistance and elevated cortisol ranges, hindering
muscle recovery. In phrases of timing, you want to
take it within the morning and ideally fasted to maximise its effectiveness.
The half-life is of two.5 to 3 days, so you’ll have
the ability to theoretically take it another time of the day.
Needless to say, T3 just isn’t a magic tablet and it will require severe dieting, exercise
and cardio to provide optimal results.
Nonetheless, we’ve observed this unconventional stack to be an effective bulking
protocol, as Dianabol will increase muscle mass and Anavar
simultaneously prevents fats accumulation. Only
intermediate or advanced users typically take the above stack because of Winstrol’s potential
deleterious effects. We have noticed this duo produce notable fats loss and reasonable
will increase in lean muscle mass, starting from 10 to 20 pounds.
For this purpose, you truly need to speculate a while in educating yourself
on the many items obtainable. This method you can piece together an efficient stack for
reaching weight reduction. Eddie Johnson is an ex-bodybuilder,
fitness addict, writer, editor and founding father of Anabolic
Our Bodies. Also a proud father of two boys and keen about
bodybuilding, diet, and the science behind modern-day supplementation.
Winstrol, when stacked with further oral steroids, will increase the chance of jaundice or liver
cholestasis. Anavar and testosterone are among the least harmful anabolic steroids with regard to ldl cholesterol.
In our expertise, the cardiovascular strain of Anavar is
marginally larger than that of testosterone.
This could be attributed to Anavar being
an oral drug, therefore inhibiting estrogen conversion and
subsequently activating hepatic lipase.
It may help to extend vitality expenditure and fats oxidation when exercising and at rest.
Studies additionally present will increase within the hormone leptin which helps to promote emotions of fullness.
General, the Legion Phoenix Fat Burner is a great natural
supplement alternative with a lot of elements and wonderful transparency.
Whether Or Not you’re doing all your women’s full-body workout or men’s bro break up, it has one thing
to supply for everybody.
A person with a better physique fat could observe decreased results with this cycle, as although it will induce weight reduction, its diuretic effects could be obscured by elevated fat shops.
One of the most potent bulking combos we now have encountered is the cycle above.
It combines three powerful mass-building steroids concurrently, causing important results
by method of muscular strength and hypertrophy. Vital hepatotoxicity from Winstrol necessitates comparatively temporary
cycles to forestall extreme liver injury.
A. With adherence to an excellent nutrition and fitness regimen, the outcome achieved
through CrazyBulk products could be sustained by people. A.
For best results, use CrazyBulk supplements with a correct diet and train routine.
The manufacturer recommends a minimal of four weeks, while many users expertise nice leads
to 2-3 weeks. Crazy Bulk presents bulking and slicing supplements together with a recent vary of SARM supplements.
Encouraging exploration of these alternate options can positively impression patient health and well-being.
Different remedies, together with S-adenosylmethionine, green tea,
frankincense, and capsaicin, also can assist inflammation management.
It’s important to note that pure alternate options usually have fewer unwanted facet effects compared to corticosteroids like prednisone.
Consulting healthcare professionals might help determine one of
the best regimen. Medicines similar to methotrexate and anti-TNF
drugs may be focused alongside these natural alternatives to scale back dependency on prednisone.
Nonetheless, prednisone may cause unfavorable unwanted facet effects, such
as stomach pain, unwanted hair development, fluid retention, complications, and extra, as nicely as serious side effects , corresponding to
hypertension, steroid psychosis, and muscle harm.
Contemplating these antagonistic unwanted effects, some patients might choose a much less pharmacologic approach, especially if
they need a solution for long-term use.
Illegal anabolic steroids are sometimes the go-to technique
for building muscle and strength, despite their critical and doubtlessly harmful unwanted side effects.
That Is the place a authorized steroid substitute is available in as the
right answer. Pound for pound one of the most potent anabolic steroids you can buy,
but discovering a safer different is crucial to our total well being.
D-bal max offers your body and muscle tissue
with every thing it needs to grow stronger. Decaduro is certainly one of the most potent steroid alternatives to allow
the constructing lean muscle for efficiency, increased metabolism and even fat loss.
The growing number of optimistic CrazyBulk critiques and success tales is a testomony to the
effectiveness of natural muscle-building dietary supplements.
From increased vitality to faster restoration and impressive positive aspects, CrazyBulk has turn into a dependable partner in the
pursuit of fitness goals-without compromising well being or security.
While these medical interventions should involve some degree of invasiveness,
they’ll supply a substitute for the repeated use
of cortisone injections for people in search of long-term ache aid.
By addressing the underlying musculoskeletal points via targeted bodily therapy and exercise,
many patients have been in a position to achieve long-term
pain relief without the need for cortisone injections.
When used too often, cortisone injections can disrupt the
body’s natural ability to regenerate and repair damaged tissue, inflicting the cartilage and
other body elements to interrupt down quicker.
The inclusion of l-carnitine makes this check booster a critical pre-workout and excellent for weight loss.
The Primary ingredient in anadrole is tribulus terrestris –
which has been studied since the early Nineteen Seventies as a testosterone amplifier and a major contributor to male virility.
Relying in your total physiology you could experience pores and
skin issues, such as acne, speedy hair progress, hair loss and edema.
Many Winstrol users could experience erectile dysfunction, testicular atrophy, insomnia, immune dysfunction and rather more.
Arnold Schwarzenegger is the most well-known bodybuilder to ever admit to
steroid use.
This is as a end result of this steroid has the power to prevent
your physique from producing pure estrogen. These opposed occasions, nonetheless,
are uncommon and usually occur when dosage limits are exceeded.
Another intriguing profit related with mesterolone is its capacity to help in the therapy
of impotence or erectile dysfunction. If a man’s T ranges are
elevated, he may uncover that he has a greater ability to take
care of an erection, especially if he usually suffers with
this ability. If you’ve got switched and see worsening signs or extra asthma assaults, contact your well being care provider, Dr.
Feldman advises.
To sum it up, mixing completely different weight and resistance coaching strategies into
your routine will tremendously higher muscle progress and strength.
Necessities like progressive overload, taking creatine, and sustaining the correct type play an enormous
position in enhancing strength coaching. A detailed study in 2018 confirmed mixing
protein supplements with resistance exercise can grow muscular tissues more.
With over a hundred illness education movies produced by the
group at Johns Hopkins Rheumatology. A practical, science-backed dosage is essential for attaining your required features safely.
Buying from a well-respected model like CrazyBulk minimizes your threat of receiving underdosed, pretend, or harmful merchandise.
Clenbutrol is most effective when paired with common HIIT (High-Intensity Interval
Training) sessions and a calorie-controlled diet.
That is why it is a lot safer to make use of a pure different to anabolic
steroids to create pure protein synthesis and muscle progress.
As we’ve explored on this information, the landscape of muscle
building in 2025 is evolving quickly. Fitness lovers are extra knowledgeable than ever, seeking solutions that combine security, effectiveness, and pure components.
CrazyBulk’s authorized steroid alternate options have
emerged as a clear answer to these needs, offering a path to
natural muscle growth and performance enhancement with out the
dangers of anabolic steroids make you gain weight (https://kino-fada.fr/pages/dianabol_acheter_en_ligne_1.html).
Legal supplements closest to steroids work by using natural elements that mimic the
effects of anabolic steroids without the dangerous unwanted facet effects.
These supplements are designed to enhance muscle development,
enhance energy, improve endurance, and assist in fat discount.One in style legal complement is D-Bal.
However, within the bodybuilding world, Masteron is mostly used as a bulking
steroid. This reveals that Masteron is a popular complement amongst bodybuilders looking for to increase strength and lean muscle mass.
Turinabol has been used as an effective anabolic steroid since
the Nineteen Fifties. It was the primary orally lively anabolic steroid to be commercially
accessible, and it is still widely utilized in bodybuilding and professional
sports activities today. It has a lot of benefits, together with faster recovery times, more noticeable
muscular growth, and elevated endurance. To assess
the position of vamorolone and dexamethasone on cytokine expression in vitro,
murine glioma cells [20] have been treated with vamorolone, dexamethasone, and DMSO (vehicle control) for
6, 12, 18 and 22 hours, as described within the Strategies.
MRNA expression profiling revealed lowered levels of all 3 cytokines after 12 hours of therapy with both dexamethasone and
vamorolone (Supplementary Determine S1).
It was hypothesized that the increased stiffness
might have been related to formation of crosslinks between adjacent
collagen molecules within the coronary heart.
Others have advised that anabolic steroid use could suppress the increases usually proven in myocardial capillary density following extended endurance training (Tagarakis
et al., 2000). However, there are a selection of interpretational points with
this research. In addition, the train stimulus employed (prolonged endurance training) is
not the first mode of train incessantly used by anabolic steroid customers.
Following these tips will enhance your train plan for a whole
strength-building workout. Using strategies like progressive overload makes
muscular tissues develop by adding challenges. This means slowly upping the load,
how usually you train, or the reps in your routine.
Creatine, a well-known substitute, can enhance strength and assist muscle tissue recuperate in just a week.
One notable exception is nandrolone, which is transformed into dihydronandrolone (DHN)
by 5α-reductase. Nonetheless, whereas testosterone is converted into the stronger androgen DHT by
5α-reductase (21), the conversion of nandrolone into DHN yields an androgen with significantly decrease binding affinity for the AR (77, 78).
Thus, whereas testosterone’s actions may
be amplified in tissues expressing 5α-reductase, nandrolone’s actions might be diminished (21).
On the basis of this metabolism, the mix of a 5α-reductase inhibitor with
nandrolone seems notably misguided.
The length and depth of PCT may vary relying on elements such because the types of steroids used, cycle length, and individual response.
Consulting with a healthcare professional is essential for creating an applicable PCT protocol.
And once customers stop taking steroids, they can have withdrawal signs similar to lack
of urge for food, tiredness, restlessness, insomnia, mood swings, and melancholy.
Whereas steroids have an result on the bodily well being of the individual,
not everyone is conscious of how a lot your psyche will suffer because of
too many corticosteroids or anabolics in your system.
This is the personality change one may expertise as a
outcome of taking anabolic steroids. Many individuals discover themselves becoming hostile, experiencing
main mood swings, and fascinating in aggressive habits, per the
DEA. This can generally lead to melancholy and suicide
as quickly as the steroids have been stopped.
Many SARMs — particularly Ostarine and RAD-140 — enhance
restoration, joint integrity, and endurance, allowing customers
to train tougher, extra frequently, and with more intensity whereas on cycle.
Steroids like testosterone act systemically, affecting muscle, reproductive tissue, the mind, liver, and
extra. SARMs, by contrast, Are Growth Hormones Steroids (https://Www.Obekti.Bg) designed to be tissue-selective, concentrating on muscle and bone while largely avoiding prostate, skin, and hair follicles.
Masteron’s dry, vascular look pairs well with the
deep muscle fullness that LGD delivers.
It can typically take a quantity of months after stopping your PED cycle earlier than your regular
menstrual cycle resumes. Some girls will
discover a quick recovery of normal cycles; this will depend upon the
individual and which PEDs were taken. By far, the
most crucial and concerning facet impact for males
utilizing steroids is the finest way the introduction of
synthetic hormones into the body slows down or typically shuts down, the traditional functioning that produces testosterone.
As Soon As the steroids are stopped, the body is now not receiving the
bogus hormones, and the person is left in a state of very low or even no testosterone.
Steroid customers will typically use this kind of injection when utilizing other kinds of compounds like
HGH, peptides, HCG, and insulin. Subcut injections usually are not as suited for oil-based
options as most steroids however work nicely with water-based compounds.
The most typical muscle injection websites are
these of the larger, stronger muscle tissue like the thigh and buttock.
For the fakes, the expiration dates will be printed on the original printing on the package.
But for actual steroids, it will by no means be the case, as the
expiration date will be added later to the unique printing on the packaging utilizing a stamp.
When stacking each, base your timing totally on the longest-acting compound in the
cycle. To mitigate these results, help supplementation (like krill oil) and a food plan rich in fiber and omega-3s are
important. The ADF acknowledges the Traditional Custodians of the
lands across Australia upon which we work. We recognise the
continued connection of First Nations people to the land, the waterways
and to neighborhood and kin, and pay respects
to Elders previous and current. In the United Kingdom, AAS are classified as class C drugs, which places them in the same class as benzodiazepines.
Through the official website, the person bottles for the merchandise reviewed right here
vary from $54.ninety nine to $61.99. The stacks begin at $179.99, which often makes them probably the most economical option. You can order directly from the manufacturer’s official website, making certain product authenticity, freshness, and entry
to particular offers—all with out stepping foot in a pharmacy or
clinic. Nevertheless, when you have existing medical situations
or are taking different medications, it’s always sensible to speak along with your healthcare
provider earlier than beginning any new complement. Many reputable brands, like CrazyBulk, additionally provide
bulk-buy savings, coupon codes, and free worldwide shipping—making these
dietary supplements accessible and cost-effective for most budgets.
Take 4 capsules of Testo-Max with water in the morning 20 minutes earlier than your breakfast.
Take three capsules of Trenorol with water forty five minutes prior to your most intense exercise of the day.
Sure dietary supplements like milk thistle are additionally generally used
to assist liver health, though their effectiveness remains to be debated.
Because of considerations relating to the increases in estrogens
observed in men after DHEA and A’dione ingestion, there was an increase within the variety of merchandise containing A’diol.
Like A’dione, A’diol is converted from DHEA and is a direct precursor to testosterone.
Unlike A’dione, A’diol cannot be immediately transformed to estrogen, as
it must first be transformed to testosterone, which might then be converted to estradiol.
After every week of taking it, I began to expertise explosive energy and shorter restoration times,
making my workouts much more productive. Not Like steroids, TestoPrime helps your body produce
the optimum amount of testosterone in your age. By the second week,
I noticed an actual spike in my energy levels, with a 10 lbs.
Sustanon is a brand name for a combination of 4 testosterone esters used to
treat low testosterone levels in males.
It is important to comply with the law and only use oral steroids as directed by a healthcare professional.
If you have any questions about the legality of utilizing
oral steroids, it is best to seek the assistance of
with a lawyer or a healthcare professional. Oral steroids are legal when they’re prescribed
by a physician for a reliable medical condition. Nonetheless, it is unlawful
to possess or use oral steroids without a legitimate prescription.
Superdrol is an oral steroid muscles vs natural muscles (vegetalid.fr) that could possibly be a DHT derivative (similar to Anadrol).
It was once incorrectly marketed as a prohormone (in the early 2000s).
Primobolan is usually stacked with different compounds for enhanced outcomes,
corresponding to trenbolone or halotestin (when cutting).
We have discovered the benefits vs. side effects ratio of Primobolan to be
optimistic, therefore why users can cycle it
for sustained intervals (up to 10 weeks).
Despite being an oral steroid, Anavar also doesn’t pose significant dangers to the liver in therapeutic dosages,
as the kidneys help to process Anavar, taking the pressure and workload off.
Tbol does not aromatize, and thus it causes no water retention and decreases the risk of gynecomastia forming,
which is the opposite of Dianabol. Arnold Schwarzenegger and other bodybuilders back in the Seventies commonly
stacked Deca Durabolin with compounds such as Dianabol, helping to create a extra pure and aesthetic
look.
Stacking two oral C17α-alkylated steroids like Anavar and Superdrol
is strongly discouraged because of compounded liver strain.
D-Bal is a legal efficiency enhancer that encourages using
a pure food regimen and common train for spectacular results.
Many things can influence how well your androgen receptors regulate and use hormones, similar to medicine, earlier steroid use,
and genetics.
Its gentle nature signifies that we want to use Primobolan at the next dosage degree than might
be the case with most other steroids, and this will embrace beginner customers
as well. The good news is that even at these greater efficiency enhancement doses,
Primobolan does not present huge aspect effect risks and should be properly tolerated
by newbies. Primobolan (Metenolone) is one other in a long line of
outstanding dihydrotestosterone (DHT) derived anabolic steroids.
It’s been said that Primobolan was a popular steroid utilized by Arnold
Schwarzenegger in his prime, and this is probably one of many causes it stays
popular with bodybuilders right now.
Thus, by containing completely different esters, it’s both fast-acting and slow-acting.
In real-life terms, this means it’s going to kick in fast,
require frequent injections (every 2 days), and remain in your system for a prolonged time
because of the presence of decanoate. Users will need
to wait a little longer for them to kick in; nevertheless, this
type of testosterone is commonly snug and enjoyable for novices to take.
Propionate could appear to be low cost; nevertheless, it is dosed at only 100 mg/ml, whereas other forms of testosterone are commonly dosed at round 250 mg/ml.
Testosterone produces distinctive positive aspects without excessively
harsh side effects.
Furthermore, probably the most advantageous steroid cycle for a male could additionally be distinct from that of a female, as women are inclined
to keep away from compounds that induce virilization. There aren’t any greatest steroids in relation to having optimal well being,
as each single anabolic steroid may cause several adverse
reactions. Superdrol is probably the most effective steroid for strength; nonetheless, its side effects are additionally harsh.
Our patients typically use a liver assist complement, SERM, and a powerful PCT for hurt discount on Superdrol.
This can mislead customers into believing that Primobolan is likely one of the stronger steroids when, truly, it’s generally regarded
as one of many milder choices available. Primobolan is favored for
its mild anabolic results and low risk of unwanted side
effects. HGH promotes fats loss, muscle retention, and total bodily rejuvenation.
It’s utilized in slicing cycles for its anabolic and anti-catabolic effects.
Equipoise increases purple blood cell production and supplies
steady muscle features with fewer side effects. Stacks additionally assist target
multiple features of muscle growth at once, from protein synthesis and nitrogen retention to recovery and endurance.
To ensure the best and safest outcomes, it’s necessary to speak to your physician in regards to the moral concerns of steroid use.
Keep In Mind, it’s always essential to seek the
advice of with a healthcare skilled earlier than starting any new supplement regimen. With the proper combination of natural products and skilled
advice, you can attain your muscle-building objectives the wholesome method.
Prescribing steroids solely for muscle acquire or athletic performance enhancement is taken into account unethical and can result in revocation of
the physician’s license to practice. Medical Doctors may legally prescribe steroids like testosterone to treat identified circumstances
of hypogonadism or other disorders inflicting low testosterone.
Docs usually use corticosteroids in an urgent care setting or
hospital to cut back acute inflammation. In The Meantime, rheumatologists and gastroenterologists often prescribe oral
steroids or present injections for arthritis and irritable bowel syndrome (IBS), respectively.
Anavarol’s finest stacking options, in our experience, are Clenbutrol, Winsol,
and/or Testo-Max. We find that Testo-Max is finest used in bulking cycles, maximizing testosterone levels and mass gain. Nonetheless, additionally it
is an efficient chopping steroid, serving to
to extend fats burning whereas sparing muscle size.
You ought to just bear in mind to are using efficient contraception when taking this treatment and let your doctor know instantly should you turn out to be pregnant while on this medicine.
Throughout your oxandrolone treatment, you will want to get regular blood and urine exams.
This is to make sure that you are not affected by any serious unwanted effects attributable to
the oxandrolone. This will stop any problems from becoming very serious since they will be caught early.
To obtain your full potential, it’s essential
to prioritize your health and well-being by specializing in proper coaching, vitamin, and recovery – without the usage
of steroids. Understanding this risk is crucial
for anyone contemplating hormone remedy. Doctorsa connects you with licensed online docs
around the clock so you presumably can rapidly kind out
your medical needs. As quickly as you ship in your request,
it’s instantly acquired by the medical doctors who’re on responsibility at that second.
It doesn’t matter if it’s late at evening, early on a Sunday morning, and even on October fifth when Bodrum celebrates its Liberation Day—there’s all
the time somebody ready to help.
Not all remedies or services described are coated advantages for Kaiser Permanente members or offered as providers by Kaiser Permanente.
For a listing of coated benefits, please check with
your Evidence of Protection or Summary Plan Description.
For really helpful remedies, please seek the advice of along with your health care
supplier. Your physician may ask questions on your fitness activities and what kinds of dietary
supplements and different substances you use.
Lets face it alcohol causes more hurt than steroids
ever could and it is legal after 21. However I think
this complete illegal steroid mess is just because this country is so fanatical about who can carry some pigskin across a a line a 100yrds away.
It’s important to research totally different suppliers and check their costs, making certain that the price includes medical support and monitoring.
Whereas these unwanted aspect effects are
usually minimal when utilizing a excessive quality testosterone product like the one bought at Fountain TRT, they nearly by no means
occur when working with a qualified online TRT doctor.
They have been studied for decades, and scientific research clearly exhibits they ship great outcomes with comparatively few unwanted effects.
Getting started with Fountain TRT and obtaining your
authorized testosterone prescription is extremely
simple. They have a harder time recovering from intense exercises, their sex
drive starts to crash, and they just don’t really feel like themselves anymore.
The doctor might do a bodily examination and order urine and blood exams.
People who use anabolic steroids on a routine basis can have withdrawal
signs after they stop taking them. Symptoms embody having depression, being extremely drained, and having no desire to eat.
Prescribed steroid doses are lower than supplementational levels used by
athletes.
Get extra details about the connection between Doctorsa and the
medical providers. In addition, nandrolone is a Schedule III controlled substance under federal law.
It also means that misuse is normally a
federal offense, punishable by hefty fines and even jail
time. If you might have problems with ache, discuss to your doctor about
the simplest combination of ache aid strategies on your scenario.
For many individuals opioids aren’t needed or helpful, although some folks do
profit from these medicines despite their risks. The new
CDC guidelines might help sufferers and prescribers
discover this delicate stability. Dianabol or DBOL just isn’t
authorized within the Usa and, like different anabolic-androgenic steroids, is a
Class III controlled substance.
Sharing or promoting prescribed steroids also violates federal legal guidelines.
In addition to the dangers to physical and psychological well being, utilizing
anabolic steroids without a prescription can have legal penalties.
In the Usa, possession of anabolic steroids with no prescription is a federal crime, punishable by imprisonment and fines.
Risks and Consequences of Using Anabolic SteroidsWhile anabolic
steroids might have some respectable medical makes use of, they can also have critical unwanted effects when misused.
The long-term results of anabolic superdrol steroid use aren’t absolutely understood,
however they will include liver harm, kidney harm,
high blood pressure, and an increased risk of coronary heart attack or stroke.
Save Well Being LLC is solely liable for finding prescription discount card
pricing for eligible prescriptions. Any drug-specific exclusions are decided by each prescription discount card vendor
and not SaveHealth or Save Well Being LLC.
As with any trade there are the nice bad, the dangerous and the downright ugly.
An example of this is Hi-Tech Pharmaceuticals 1-AD, which is basically
a legal pre prohormone – containing 1-Andro – on the US market right now.
Additionally, products which may be legal or unlawful now might or
is probably not in the future. Be conscious that anything we
post is for academic functions and isn’t recommendation or steering on the use or procurement of those hormones/drugs.
The Ajuga Turkestanica plant, the place turkesterone is derived from, is taken into account
to be adaptogenic as it has been linked with a spread of therapeutic makes use
of together with heart safety and sustaining
aged skeletal muscle (5, 6). Bear In Mind, the
trail to a muscular physique is a personal one, and
what works for one may not work for one more. If you’re
nonetheless growing, you shouldn’t mess with hormone supplements.
Your body is still attempting to figure out how it’s going to perform.
These compounds, when taken by mouth and metabolized by the liver, are reworked into anabolic hormonal substances.
Many people choose to take natural dietary supplements, like zinc or pine pollen, that can restore
testosterone levels and increase the body’s degree of testosterone manufacturing during their post-cycle therapy.
While even these items can intervene with testosterone manufacturing over the lengthy run, they
will actually reduce the impression of a spontaneous drop in testosterone ranges, like one would experience
after stopping a cycle.
Observations of aggressive behavior caused by AAS
use are described in human and animal research [81, 82].
Aggression could be linked with anxiety in animals and involves a number of brain circuits which are affected by AAS [83].
Animal research confirmed impression on the glutamate, the GABAergic, the serotonergic and dopaminergic
system as nicely as on tachykinin and encephalin pathways [84-88].
In quick, these substances are not anabolic steroids, but once ingested convert to supply an anabolic steroid motion. Nonetheless, while this is the purpose of
a prohormone, some dietary supplements that carry the prohormone label have been nothing however an anabolic steroid that requires no conversion. The popular Superdrol is maybe the
best example of a steroid being labeled a prohormone.
You should also spend much less time sitting and gradually increase the intensity of your exercise over
time.
So, having something between anabolic steroids and testosterone boosters is appealing.
Each SARMs and prohormones are powerful PEDs (performance-enhancing drugs) that may
allow you to achieve your goals. Early research means that SARMs are extra tissue-selective than traditional steroids, meaning they target muscle tissue more successfully while minimizing
effects on different organs. This leads to a safer and extra
tolerable profile for athletes and health fanatics.
Stacking and biking are superior methods that may probably amplify
your results. However tread fastidiously, as these
methods come with elevated dangers and require meticulous planning.
The prohormone panorama is a minefield of hype, half-truths, and
potential well being hazards.
When it involves prohormones, you should cycle them
accurately to reap their advantages. Pro-hormones can have unwanted aspect effects
that will differ from person-to-person and from product-to-product and
are most likely not protected to use for lengthy
periods of time. They are also linked to cardiovascular problems, acne, and prostate points.
The effects of pro-hormones rely upon whether or not they
act on the estrogen and progesterone receptors within the physique.
This can embrace an increase in sodium and water retention, which may lead to hyperhydration which can result in hyponatremia.
Some federations, including Strongman, Crossfit, and Bodybuilding, for instance, could not permit them and neither does
the military.
Nevertheless, they can even have some serious side effects identical to
anabolic steroids are a type of.
Selective Androgen Receptor Modulators (SARMs) are an thrilling development in performance enhancement.
SARMs offer a possible alternative to prohormones, with
the promise of comparable muscle-building and fat-burning effects however with a extra targeted
strategy that may scale back the chance of side effects.
Prohormones essentially present your body with an additional provide of raw materials to ramp up
pure testosterone production. This can result in the fascinating
effects mentioned above, but it’s not without potential drawbacks.
As Soon As a cycle ends, natural testosterone needs to get well with the assistance of post cycle therapy.
Gary David is the founder and CEO of CrazyMass,
one of many nation’s main complement firms.
Men can also experience issue reaching or sustaining an erection as a result of decreased testosterone levels.
Different physical symptoms embrace lowered vitality ranges,
increased body fats, and decreased muscle mass. Mood modifications
such as depression and irritability may be current in these with low testosterone.
Using anabolic steroids such as Trenbolone (Tren) could cause
modifications in hormone levels, which can result in testicular shrinkage.
This is a typical problem among bodybuilders and athletes who use
anabolic steroids, and it might be a dangerous
facet impact of these medicine.
Testosterone performs a job in regulating mood, and when levels
are low, it might possibly lead to a range of emotional signs.
Low vitality ranges and a common sense of lethargy are
additionally widespread among males with low testosterone.
Anabolic steroids, particularly testosterone and its artificial derivatives, have a extra complex relationship with penile size and performance.
It is crucial to do not neglect that penis size does not necessarily correlate with sexual satisfaction or efficiency.
Many different elements, such as emotional connection, communication, and method, play a extra
important position in sexual satisfaction for each companions.
Nonetheless, it is important to notice that testosterone alone
doesn’t determine the scale of the penis. Other components, corresponding to the amount of testosterone produced, the sensitivity of the
penis to testosterone, and the body’s response to the hormone, additionally
play a job in penis development.
When it involves bodybuilding, one of the well-liked
subjects of discussion is the usage of anabolic-androgenic steroids, similar to trenbolone.
Many individuals have heard concerning the potential unwanted effects of using such medication, including the possibility that they’ll trigger testicular shrinkage.
The hormone testosterone is responsible for the event of male
sexual traits similar to physique hair, muscle mass, and genitalia measurement.
While Tren is a type of anabolic steroid that can increase testosterone ranges within the body, it will not
directly trigger your testicles to shrink. They can consider your signs and perform
applicable checks to determine in case you have low testosterone ranges.
If diagnosed with low testosterone, there are various remedy options
available, including testosterone replacement therapy, which can help restore hormone levels and
enhance sexual well being. In conclusion, there is restricted scientific proof
to help the declare that injecting testosterone can result in a smaller penis.
However, using an extreme quantity of Trenbolone can result in unfavorable unwanted effects, together with Tren Dick.
It’s essential to make use of Trenbolone responsibly and to comply with recommended dosage tips.
One possibility is prescription medications, such as
phosphodiesterase kind 5 (PDE5) inhibitors.
In conclusion, whereas low testosterone levels can contribute to penile shrinkage, there are a number
of different factors that may additionally play a role.
Poor blood circulation, psychological factors,
extreme weight gain, and getting older can all impact penile measurement and function. It’s necessary to take care of a wholesome life-style,
talk with a healthcare provider about any concerns, and focus on overall sexual
satisfaction quite than solely on penile dimension. In conclusion, testosterone substitute therapy
can have a optimistic impact on libido and erectile perform
in males with low testosterone levels. However,
individual results could range, and it is necessary for males to discuss the potential advantages and risks with their healthcare supplier before starting
remedy. Additionally, life-style changes and different remedy choices may be helpful in bettering sexual health.
Bear In Mind, it’s necessary to prioritize overall sexual health and satisfaction somewhat
than focusing solely on measurement. During puberty, hormones,
including testosterone, play an important position within the development of secondary sexual
traits, together with penis progress. Testosterone is a hormone produced
by the testes and is responsible for male characteristics such as muscle
improvement and deepening of the voice. Testosterone
is the primary male intercourse hormone that plays an important role in the improvement and upkeep of male reproductive and sexual
characteristics. It is liable for the growth of facial and body hair, changes in the voice, and the development of
muscle mass and strength. Testosterone also performs a task within the
development and upkeep of the penis.
It is liable for the growth and growth of the penis throughout puberty.
Testosterone also affects sexual operate, libido, and overall sexual well being.
As males age, the production of collagen, elastin, and connective
tissue decreases, resulting in a loss of elasticity and firmness within the penis.
It’s crucial to discuss any considerations with your healthcare provider, monitor for unwanted side effects, and
explore various remedies if needed.
Whereas the short-term advantages of using anabolic Steroids Drug definition could also be tempting,
the potential risks and consequences far outweigh any potential positive
aspects. As a bodybuilder, it is important to grasp that the
usage of anabolic steroids, including Trenbolone, is unlawful without a prescription and might
have extreme authorized and well being penalties. Utilizing Trenbolone with no prescription can lead to legal sanctions, including fines
and imprisonment. In addition to the authorized penalties, utilizing Trenbolone may cause permanent damage to your body’s organs and techniques,
including the liver, cardiovascular system, and reproductive system.
If you experience any unwanted side effects or well being concerns while using Trenbolone, it’s essential to seek
medical recommendation. Your healthcare supplier may
help you determine whether or not you want to regulate your dosage or
take a break from the steroid altogether. For some men, the
answer to higher erectile functions and satisfying intercourse could lie
in therapy with supplemental testosterone or human growth hormone.
Activin A Blockers – Experimental compounds that target the myostatin pathway to reinforce muscle progress.
Tesamorelin – Primarily used for fat loss but additionally aids in muscle preservation.
Utilizing ACE-031 responsibly within structured cycles helps
mitigate dangers and optimize advantages.
Understanding these dangers and recognizing early signs
is important for shielding long-term well being.
Anavar is widely considered the most female-friendly anabolic steroid
because of its low androgenic exercise and talent
to ship lean, defined results with out vital unwanted effects.
When used appropriately, it supplies an effective efficiency and aesthetic edge — without the majority or bloating.
Anavar can also cause masculinization in women, being extra generally noticed in larger dosages.
Moreover, combining Anavar with different anabolic
steroids corresponding to Winstrol significantly increases the probability of masculinization. She misplaced
a significant quantity of fats, particularly from the midsection, and gained notable quantities of lean muscle, which is clear by her body weight rising.
Creatine has been proven to assist build lean muscle mass and enhance power
in women, particularly postmenopausal girls experiencing muscle loss.
It is especially effective here when mixed with resistance training.
Among the noticeable outcomes, the key changes after
a protracted Anavar cycle can be enhanced muscle definition and a leaner
look.
It is a well-liked steroid because of its delicate side effects and comparatively low risk of inflicting harm to the body.
The typical Anavar cycle length what is the function of steroids 6-8 weeks, although
some folks might choose to extend it as much as 12 weeks. To deal with steroid misuse, we need a plan that
covers consciousness, prevention, and therapy.
Narcissus in other words, it was like a second of love daily to have the ability to see myself naked”. When empathy is lacking, conflicts, and/or an agitated mood can simply result. Generally, individuals get in the way of performance, and it’s usually deliberate routines that are disturbed by others e.g., when exercising. Day By Day routines such as controlling one’s physique could be time-consuming when one is preoccupied with oneself. When this stage is reached and the physique can no longer develop naturally, they feel that a cautious use of AAS is justified.
Steroids are medicine that reduce inflammation and treat varied circumstances, similar to allergies, asthma, and autoimmune issues. They are additionally used to extend muscle mass and energy, in addition to to enhance athletic performance. A cycle demanding warning is the “long cycle,” extending Oxandrolone use past 10 weeks. Whereas the physique might have time to manifest results, surpassing the everyday 6 to 8 weeks can heighten potential risks and unwanted effects, emphasizing the significance of responsible and knowledgeable utilization. With responsible use, Oxandrolone can be a valuable tool in a feminine bodybuilder’s arsenal.
It is recommended to take Anavar dosage about minutes before understanding. This will permit sufficient time for the steroid to take impact and offer you an additional boost of vitality throughout your lifts. Post-cycle lipid panels are sometimes severely skewed—HDL suppressed, LDL elevated, and triglycerides borderline. Even in case your hormones get well, these markers can put long-term strain in your cardiovascular system. A common pink flag in enhanced athletes—especially on high-dose check or during aggressive PCT. Insulin resistance will decrease SHBG and enhance danger of long-term metabolic points. If you’re using DHT-based compounds (e.g., Masteron, Anavar), or 5-alpha inhibitors (like finasteride), DHT ranges are essential to track.
My energy has continued, and I don’t really feel like I lost a lot of the tissue I gained even though I’m now in prep. I tracked macros religiously all through the cycle, so I suppose if I ate according to appetite I would have gained weight lots faster. I posted a couple of months in the past about my first unwanted effects since that is my first cycle, and I wished somebody had detailed the unwanted effects for me earlier than I began. The first step of the exercise is to shut your mouth, then suck your cheeks in and pout your lips.
For example, seized samples typically comprise harmful components or incorrect doses.
Anabolic-androgenic steroids (AAS) work by enhancing
muscle progress and strength. They enlarge muscle cells through hypertrophy, resulting in elevated muscle
mass. Muscle Cocktails is a slang time period for mixtures
of steroids. This term is usually used to check with the follow of taking a number
of forms of steroids simultaneously to maximise muscle progress and performance.
Repeated steroid injections might cause cartilage
breakdown, so a health care provider may recommend them for under short-term
use.
The second group of steroids, the androgenic/anabolic steroids, are hormones made in the body to regulate the manufacture
of testosterone in the testicles and ovaries. The pituitary gland,
located at the base of the mind, helps regulate testosterone
production and hormone secretion. Development hormone and follicle stimulating hormone (FSH) are among the many hormones that stimulate testis and ovary operate and are two of the many hormones secreted by the pituitary.
“Roids” is a broad term used for all sorts of anabolic steroids.
“Juice” refers to oral and injectable forms,
capturing the essence of pumping something powerful into your body.
“Gym candy” highlights how these drugs are perceived as enhancements for gym-goers, making them sound nearly like a treat quite than a potentially dangerous substance.
It is commonly utilized by bodybuilders and athletes to extend muscle mass and enhance performance.
D-Bol is thought for its fast-acting results and
is commonly used in bulking cycles. Anabolic steroids embrace the hormone testosterone and related medication. Anabolic
steroids have many physical effects, together with promoting muscle progress and growing energy and power.
Thus, these drugs are sometimes used illegitimately to achieve a aggressive edge in sports.
Roughly 2% of females and 6% of males worldwide use or abuse anabolic steroids,
with comparable estimates for the Usa. This term refers to
anabolic steroids, which are synthetic substances that mimic the effects of
testosterone within the body.
Sadly, as a result of corticosteroids are derived from cortisol,
they not solely treat a variety of illnesses, but additionally affect the physique in varied methods while doing so, a lot of which aren’t pleasant.
In different words, although prednisone could be an extremely useful drug,
it where can you get steroids also create many unwanted side effects.
A person could wish to discuss with a physician if their present remedies aren’t helping with their
arthritis symptoms. Corticosteroid injections mimic the hormone cortisone, which the body makes naturally.
Arthritis therapy typically includes corticosteroid,
biologic, and PRP injections.
Steroids are ldl cholesterol derived with male hormones similar to testosterone and other forms of artificial testosterone and other synthetic kinds of hormones.
The probabilities you experience unwanted facet effects goes up the
longer you take them, particularly if you use them for an extended time.
Your supplier will allow you to understand the dangers and
advantages before you start any new medication. For example, steroids might prevent the kind of worsening
of kidney irritation that may cause kidney failure in individuals who have autoimmune illnesses
like lupus or vasculitis. They could help these
individuals avoid needing kidney dialysis or a transplant.
Certain vaccines, similar to these for measles, mumps, and tuberculosis, can have harmful interactions with corticosteroids.
Different vaccines, similar to those for flu or pneumonia, may not work as nicely if an individual is also taking
a high dosage of a corticosteroid.
Around 5 out of each one hundred individuals (around 5%) expertise critical
psychological well being problems once they take
steroids. Let your healthcare staff know if you
notice any changes in your emotional or psychological wellbeing.
Additionally allow them to know when you or any members of the family have ever had melancholy or manic melancholy
(bipolar disorder). They verify your ranges of blood cells and other substances in the blood.
In practice, we see testosterone leading to barely less weight
achieve than Dianabol, but it’s going to construct an identical quantity of lean muscle tissue.
The other major distinction is that testosterone has a
stronger reaction with the 5α-reductase enzyme,
resulting in heightened levels of DHT (3). Thus, bodybuilders have the choice to use an AI (aromatase inhibitor) to
inhibit estrogenic-related unwanted aspect effects of Dianabol, stopping gynecomastia and water weight (2).
Common AIs used are anastrozole and letrozole; however, we find them to
minimize back estrogen at the expense of worsening blood
strain ranges. Corticosteroids effectively suppress the immune system and reduce irritation.
For occasion, you often need to wait a minimal of three months between injections in the same area.
Medical Doctors additionally suggest no more than four injections in the
identical area within a year. It’s essential to follow your doctor’s recommendation and attend
any follow-up appointments. This ensures that
any side effects are caught early and managed effectively.
Bruising across the injection site is another possible aspect impact.
This occurs as a result of the needle can cause minor bleeding beneath the skin. For example, a marathon runner experiencing extreme
knee pain simply days earlier than a race would possibly
discover fast reduction from a cortisone shot, permitting them to take part with out discomfort.
You know, simply to make positive that everything went fantastic and you
weren’t affected by any potential unwanted side effects of detox products.
If you’ve problems with medicine and need help, or
in case your family members show warning signs of drug habit, you may need to consider using rehab
services. Rehabs are specifically designed to help folks cope with a wide spectrum of issues regarding drug
use and start a new life, a happier and more healthy one. We also wish to
emphasize that you simply shouldn’t be afraid of stigmatization as a outcome of all services supplied
by rehabs are strictly confidential. Stimulants enhance mind exercise, improve alertness
and enhance attenion. These effects permit folks to get ‘high’ and finally trigger habit.
We provide responsive buyer help that may resolve your queries instantly.
We provide many steroids for sale on the highest high quality potential (pharma-grade).
All the merchandise are manufactured in full compliance with world high quality requirements.
Testosterone can enhance the anticoagulant motion of warfarin.[18] Critical bleeding has been reported in some patients with this drug-drug interaction. Although the mechanism is unclear, testosterone might reduce procoagulant
elements. Reduction of warfarin dosage could
also be needed if testosterone remedy is coadministered.
As a end result, we get a steroid with low (but nonetheless existent) androgenic effects.
Steroid injections may be utilized for joint issues and rheumatoid joint ache.
They can likewise be utilized for certain circumstances influencing delicate tissues, just like ligament irritation or tennis elbow.
Win-Max is particularly valued by these wanting to undertake serious slicing phases pros and cons of anabolic steroids,
Una, elite athletes who wish to take advantage
of superb boosts in efficiency and power, which
enhance energy, endurance, and pace. High levels of
cholesterol can increase your risk of experiencing
a stroke or coronary heart illness, so the cardiovascular unwanted side effects of Winstrol are too significant to disregard.
Stanozolol can and can improve bad cholesterol levels (LDL) and decrease
good cholesterol (HDL) ranges. Low-dose medical research present a very clear negative effect on cholesterol with
alarming adjustments to the LDL/HDL ratio[2]. So, we
will solely imagine what higher doses can do to our levels
of cholesterol.
These steroids will present speedy outcomes that may deliver about a very quick body transformation in a brief and sharp 6-week cycle.
As with all oral steroids, the toxic effects on the liver make it unsuitable and probably harmful to take for longer than eight weeks.
It’s not simply the liver you should fear about with
an extended Winstrol cycle. The other cause not to exceed an 8-week
cycle is Winstrol’s impact on ldl cholesterol.
This means a dosage of 5mg day by day is as excessive as many women will need to go – and this completely finds Winstrol dosage is more than capable
of delivering excellent results. If you could have
successfully used a 5mg dose whereas responding well to Winstrol
and without masculine traits creating, trying 10mg daily isn’t out of the query for females.
However this isn’t a dosage to begin when utilizing Winstrol
for the first time, and you need to already be assured
in using 5mg before doubling the dose for your next cycle.
Periodically, patients receiving testosterone ought to have their hemoglobin and
hematocrit concentrations measured to detect polycythemia.
At Maxlabs.co, we assure the security and high quality of every of our products.
We be certain that we source goods only from dependable manufacturers with a reputation for the high-quality manufacturing of pharmaceutical medicine.
The research also showed that these adverse modifications reversed themselves after 5 weeks of ending
use of the steroid – again, this was at a low medical dose.
Unnecessary to say, you need to pay close consideration to
your cholesterol when utilizing Winstrol. If you could have existing excessive
ldl cholesterol, you’d be taking a big danger in using Winstrol in any respect.
Regardless Of this, even very low doses have been shown in studies to result in over a 50%
lower in testosterone production in simply
two weeks.
It doesn’t intervene with the all-natural manufacturing of testosterone degrees.
Anavar boosts healthy protein synthesis within the body, improves bone
thickness, as well as promotes the event of muscle mass.
When handled with an empty abdomen, you’ll be able to obtain maximum outcomes.
A grainy look is very desirable for opponents,
and Winny can deliver that. Though the graininess and other enhancements is
not going to last long run, the primary use of Winny is for
contest prep, so timing your cycles to attain most outcomes is
critical if you’re competing. To expertise the most effective that Winstrol can ship throughout
a slicing part, you want to already do every little thing you can relating to food plan and train to get lean and trim.
The goal when creating Winstrol was to design a steroid with very low androgenic exercise in comparability with
its anabolic effects, which was highly successful with Winny.
When it involves burning fat in bodybuilding, a mix of heavy coaching and cardio is efficient.
Heavy weights assist construct muscle and enhance energy,
whereas cardio aids in fats loss. Additionally, think about incorporating fat-burning exercises into your routine.
B-AET helps with fats loss by inhibiting cortisol manufacturing via the
suppression of the enzyme 11β-HSD1.
Keep Away From close contact with folks who’ve just lately had
stay vaccines taken by mouth (oral vaccines) such as oral polio or the typhoid
vaccine. If you’ve epilepsy this might become worse when taking steroids.
You would possibly really feel dizzy and you might
really feel as though the room is spinning. Let
your physician or nurse know when you have any issues
along with your eyes. If you may have diabetes already, you might
have to check your blood sugar levels more typically than ordinary.
If you do come into contact with somebody who has them, tell your healthcare team straight away.
Steroids can hide or change the signs supplements and steroids signs of some infections.
This is most likely as a result of it being a gentle compound and the kidneys processing
a part of the compound (in conjunction with the liver).
We have seen girls take Anavar safely with out creating virilization signs.
Thus, it has many benefits which would possibly be advantageous for both sexes.
Thus, Deca Durabolin is usually taken as a stack and run concurrently with different bulking steroids.
Deca Durabolin (nandrolone decanoate) is an efficient anabolic
bulking agent.
The longer you are on treatment, the extra the adrenal
glands will stop functioning and successfully go into hibernation. Some of
the more commonly prescribed corticosteroids are cortisone,
hydrocortisone, prednisone, prednisolone, and methylprednisolone.
Most corticosteroids can be found by prescription only
(with the exception of over-the-counter nasal sprays or topical steroids like hydrocortisone 1%).
Corticosteroids were first used to relieve symptoms of arthritis back in 1948 at the Mayo Clinic in Rochester, Minnesota.
The medication are artificial variations of cortisol produced
by the adrenal glands, which attach to the cortisol receptors on organs to elicit
the same effects. Also referred to as glucocorticoids or just
“steroids,” they mimic a hormone called cortisol that the physique produces
at times of stress. Steroids quickly reduce irritation and an overactive
immune response.
While there are ways to search out and confirm the quality of AAS on-line, it is essential to strategy this with warning, consciousness of the legal panorama,
and a focus on health and security. Overall, your joint well being whereas on AAS should be
a first precedence so your coaching is not hindered.
Staying well-hydrated and sustaining a balanced diet wealthy in essential nutrients
like omega-3 fatty acids, glucosamine, and chondroitin can help joint
well being. Repeatedly pursuing private information and lifting the heaviest weights can injury joints and cause
injuries. Proper stretching and warming up with lighter weights are important.
To forestall joint points when using moist AAS compounds, it
is essential to use the suitable AI dose (not too high) to handle estradiol levels and forestall
excessive water retention. Other AAS both have a impartial
influence on the joints or enhance their strength and therapeutic by boosting collagen production, with Nandrolone being a major example.
That’s how I got here up with the name of my dietary supplement I invented for people on prednisone, Nutranize Zone.
“And you’ve crossed over” into a special world of prednisone, where you are feeling like a very totally different
person. People have talked about the means it changes their eyes,
it changes their listening to capacity, causes tinnitus,
the stability, it changes your thoughts.
Injections can ship medication on to the affected joint and supply longer aid.
Present tips recommend that steroids are typically protected throughout being pregnant and breastfeeding.
Nevertheless, at all times talk about this with your healthcare
supplier before proceeding. Single steroid injections are usually thought-about secure and may be
beneficial in these situations.
Simply like the band’s music, steroids are believed to enhance energy and performance.
This term refers to steroids, particularly highlighting their ability to increase
muscle size and pump up the physique. “Pumpers” means that steroids can improve the pump experienced
during weightlifting or other forms of exercise. This time period refers
back to the act of utilizing steroids to boost athletic efficiency or bodily appearance.
It suggests that steroids can hype up a person’s skills or physique.
Thanks for sharing, Great Work👍