Day 3 of 100 Days of RTL Projects – Enhanced PWM Design-Why we need Enhanced design?

Enhancing PWM Design: Addressing Resolution and Frequency Control

In the realm of electronics and digital design, Pulse Width Modulation (PWM) stands as a crucial technique for controlling the power delivered to electrical devices. However, as with any design, there are intricacies and optimizations to consider for efficient operation. Let’s delve into a detailed analysis of PWM design and explore solutions to common issues encountered.

The core problem often arises from the limited resolution of the PWM signal. Traditionally, designers relied on a straightforward calculation, often leading to a maximum value of 255. However, this poses a limitation, as it doesn’t equate to a 100% duty cycle. To resolve this, a simple adjustment is proposed – adding a bit to the calculation, allowing for a maximum value of 256. While this exceeds the practical range, it ensures accurate computation without compromising resolution.

Enhancements Overview: In our quest to improve PWM circuits, we’ll focus on several key enhancements:

1. Increased Duty Resolution: By adjusting the duty input parameter to r+1, where r represents the resolution of the duty cycle, we can achieve finer control over the duty cycle. This enhancement allows for smoother transitions and more precise adjustment of the output signal.
2. Addition of Timer: Introducing a timer component enables dynamic control over the switching frequency of the PWM signal. This timer operates independently of the system clock, providing greater flexibility in adjusting the signal characteristics.
3. Integration of D Flip-Flop: Incorporating a D flip-flop into the design helps eliminate glitches and ensures a clean PWM output signal. By synchronizing the flip-flop with the timer, we can achieve smoother transitions and minimize signal distortion.
4. Adjustment of Counter Logic: Modifying the up counter to include the timer tick as an enable signal allows for synchronized operation with the timer. This ensures precise timing control and improves the overall accuracy of the PWM signal generation.
5. Parameterization Update: Exposing parameters such as timer bits and final value enables greater flexibility and dynamic adjustment of the PWM signal characteristics. This parameterization allows users to tailor the PWM circuit to their specific requirements and achieve optimal performance.

Understanding Duty Cycles and Frequency Control in Circuits

We’re dealing with a generic scenario where we have a range of values represented by 2^r-1, going from 0 to 2^r-1. For illustration, let’s consider r=8.

If we want a duty cycle of 0%, we simply set the value to 0. This means the signal stays at 0 throughout the cycle.

However, if we’re dealing with an arbitrary duty cycle where the maximum value allowed is 2^r-1, which is 255 in the case of 8 bits.

Now, let’s consider what happens when we set the duty cycle to the maximum value, 255. The cycle counts up to 255, stays at 255 for a bit, then resets to 0. This means the duty cycle isn’t exactly 100%.

To resolve this, we can extend the range by one bit, allowing us to represent up to 256. However, any value above 255 will still result in the output being 1. Therefore, setting the duty cycle to 256 or above isn’t practically useful.

To fix this issue, we adjust the duty cycle calculation to r+1 instead of r. This ensures that we have enough range to represent the desired duty cycle accurately.

Moving on to the switching frequency, initially, our design lacks control over the frequency. We’ll address this in the next steps of the circuit design.

Understanding the Operational Frequency of a Pulse-Width Modulation Design

When crafting a PWM system, one of the fundamental components to consider is the system clock period. This clock governs the timing of various operations within the system and is distinct from the switching frequency specific to the PWM signal. For instance, envision a scenario where a system operates on a board with a 100 megahertz clock frequency, resulting in a clock period of 10 nanoseconds.

To elucidate the operational frequency, let’s dissect the underlying mechanism of the PWM design. The pulse-switch modulation period, or simply the PWM period, defines the duration of a complete cycle of the PWM signal. This period is pivotal in computing the switching frequency, which denotes how frequently the PWM signal transitions between its high and low states.

Let’s break down the process of calculating the switching frequency for the pulse-width modulation (PWM) signal in the described circuit:

1. System Clock Period: The system operates with a clock period determined by the system clock frequency. In this case, the system clock frequency is 100 megahertz, which translates to a clock period of 10 nanoseconds.
2. PWM Period: The PWM period, also known as the pulse-switching modulation period, is the duration of one complete cycle of the PWM signal. It’s essential to determine this period to calculate the switching frequency. In this circuit, the PWM period is determined by the count range of the counter, which goes from 0 to 255 in the case of 8 bits. So, the PWM period is 256 times the system clock period.
3. Calculation of PWM Period:

• Since the counter counts from 0 to 255, or (2^r) in general, where (r) is the number of bits, the total count range is (2^r).
• Therefore, the total period of the PWM signal is (2^r) times the system clock period.

1. Switching Frequency: The switching frequency is the reciprocal of the PWM period. It represents how many cycles of the PWM signal occur per unit time, usually expressed in hertz (Hz).
2. Example Calculation: Given the system clock period of 10 nanoseconds and an 8-bit counter:

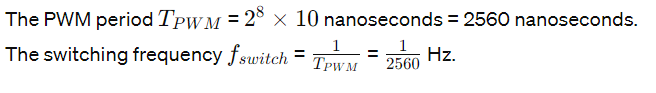
Unlocking Precision: Enhancing Pulse-Width Modulation Design for Dynamic Frequency Control

In the realm of electronic systems, achieving precision and flexibility in operational frequencies is crucial for optimal performance. Consider a scenario where an 8-bit system operates with a clock period of 10 nanoseconds due to a 100-megahertz system clock. Upon calculation, it’s evident that the switching frequency of this system clocks in at 390 kilohertz.

However, what if we seek to exert more control over this frequency, fine-tuning it to suit specific application requirements? Here’s where the enhancement of pulse-width modulation (PWM) design comes into play.

Identifying the Need for Enhancement:

To delve deeper, we first acknowledge the need for an additional component in the PWM design. This component should enable dynamic control over the clock or counter, allowing us to regulate the switching frequency effectively.

The Solution: Introducing the Timer:

The solution to our quest for dynamic frequency control is elegantly simple: the incorporation of a timer. This timer, operating at the same 100-megahertz frequency as the system clock, introduces granularity to our control over the PWM signal.

Understanding Timer Integration:

With the timer in place, the PWM period calculation undergoes a transformation. Now, the PWM period isn’t solely dictated by the system clock; it’s also influenced by the timer’s final value. This final value, coupled with the system clock period, determines the precise PWM period.

Dynamic Frequency Adjustment:

The inclusion of the timer introduces a flexible means of adjusting the switching frequency. By varying the final value of the timer, engineers can dynamically alter the PWM period and, consequently, the switching frequency.

Final Improvement: Adding a Flip-Flop:

To enhance the PWM design further, we introduce a flip-flop. This flip-flop, coupled with a comparator, enables the precise control of duty cycle. By dynamically adjusting the flip-flop’s output, we can finely tune the PWM signal’s duty cycle.