- Biologically Inspired:
- The AdEx model is designed to capture essential features of real neurons.
- It incorporates biologically realistic time constants and mimics neuronal behavior, including refractory periods and spike-frequency adaptation (SFA).
- Model Description:
- The AdEx model consists of two variables: membrane potential ((V)) and adaptation variable ((w)).
- The first equation describes the dynamics of the membrane potential, including an activation term with an exponential voltage dependence.
- Voltage is coupled to a second equation that describes adaptation.
- Both variables are reset if an action potential is triggered.
- Firing Patterns:
- The AdEx model is capable of describing various neuronal firing patterns, including:
- Adapting: Firing rate decreases over time.
- Bursting: Rapid sequences of spikes.
- Delayed spike initiation: Delayed response to input.
- Initial bursting: Bursting at the start of stimulation.
- Fast spiking: High-frequency firing.
- Regular spiking: Regular, periodic firing.
- The AdEx model is capable of describing various neuronal firing patterns, including:
- Mathematical Formulation
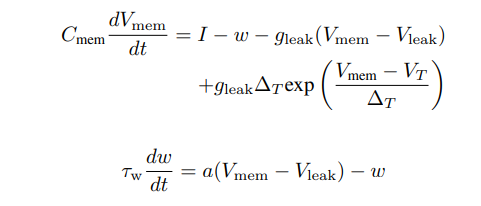
- Equations:
- Equation (1) describes the membrane potential dynamics:
- The rate of change of membrane potential dVmem/dt is influenced by external, synaptic, and inter-compartment input currents.
- It accounts for leak and exponential currents.
- Cmem represents the membrane capacitance.
- Vmem is the membrane potential.
- gleak and Vleak denote the leak conductance and leak potential.
- a represents subthreshold adaptation.
- VT is the exponential threshold, and ∆T is its slope factor.
- Equation (2) describes the adaptation current dynamics:
- The rate of change of adaptation current dw/dt depends on the difference between Vmem and Vleak.
- The adaptation variable w is updated by a current b at spike time.
- Equation (1) describes the membrane potential dynamics:
- Hardware Realization:
- For hardware implementation, the adaptation term is transformed.
- The adaptation output current w is expressed as w = a(Vw – Vleak).
- This substitution modifies Equation (2) to:
- dVw/dt = gw(Vw – Vmem).
- Dendritic Structure:
- The circuit implements controlled conductance between adjacent isopotential membranes.
- The inter-compartmental current flowing through the tunable conductance connecting two membranes is given by:
- Iic = gic(Vi – Vj), where gic is the inter-compartmental conductance, and Vi and Vj are potentials of the shunted membranes.
- Energy Efficiency:
- The AdEx model’s computational affordability arises from its subthreshold operation (all transistors operate in the subthreshold region).
- It ensures extremely low power consumption, making it suitable for energy-efficient neural circuits.
- Historical Context:
- Introduced by Brette and Gerstner in 2005, the AdEx model builds on features of the exponential integrate-and-fire model and Izhikevich’s 2-variable model.
- Read more https://ieeexplore.ieee.org/abstract/document/8419063
- About the Circuit
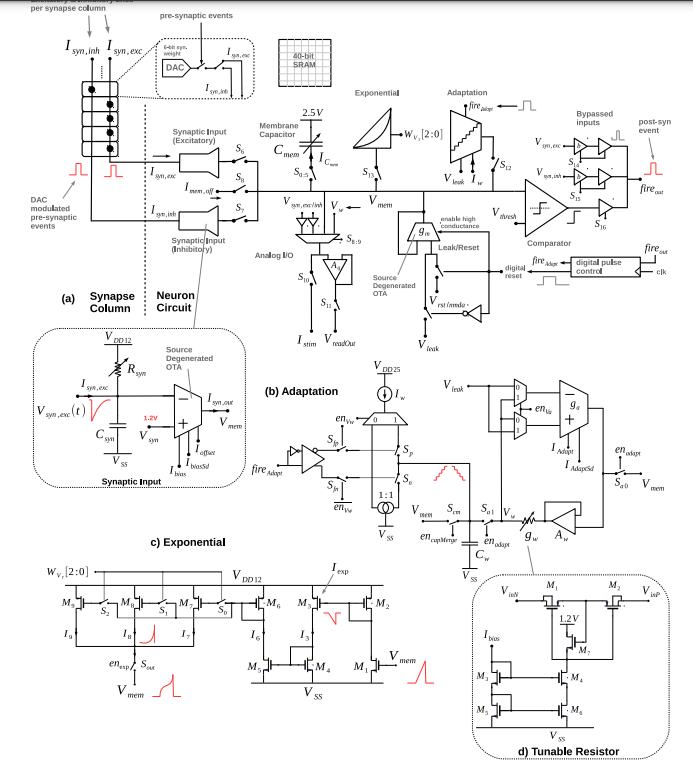
- Purpose and Functionality:
- The adaptation circuit serves to implement accelerating and decelerating spike-triggered adaptation.
- It also handles adaptation current based on equations (Eq. 3 and Eq. 4).
- Circuit Overview:
- The circuit is inspired by a first-generation design.
- A simplified schematic is depicted in Fig. 2b.
- Top Right Part of the Circuit (Eq. 3):
- The output current w is generated by an OTA (Operational Transconductance Amplifier) with conductance ga.
- It emulates the model’s subthreshold conductance parameter a.
- The OTA senses the difference between Vleak and Vw at its inputs.
- A configuration bit enVa switches them to realize negative ga.
- Lower Right Part of the Schematic (Eq. 4):
- The input current gw(Vw – Vmem) is integrated on the adaptation capacitor Cw.
- The membrane is buffered by an OTA labeled Aw.
- A tunable floating conductance gw connects the buffered membrane to capacitor Cw.
- Circuit Activation and Capacitor Merging:
- The circuit is enabled by asserting the bit enadapt and dis-asserting encapMerge.
- This connects the output to the membrane Vmem via switch Sa0 while connecting Cw to the node Vw.
- When encapMerge is disabled (e.g., in LIF mode), the unused adaptation capacitor can be merged with the membrane capacitor Cmem, effectively increasing the maximum Cmem from 2.36 pF to 4.36 pF.
- Adaptation Variable and Time Constant:
- The voltage on the capacitor Vw emulates the adaptation variable in the model.
- A tunable conductance implements the adaptation time constant τw = RwCw, where Rw = 1/gw.
- Charge Pump and Triggering:
- The left side of the circuit features a charge pump.
- An on-chip bias current Iw is sourced or sunk from node Vw via pass transistors Sp and Sn (assuming enadapt = 1).
- The circuit is triggered by the input event fireadapt, which indicates a digital spike event.
Optimised for mobile use, the site also has a desktop version. The platform employs the cutting-edge PGP protocol and operates on 128-bit SSL encryption to guarantee
top-notch security. The local regulator of internet gaming licensed
it. Rocketplay com – this is one of the company’s sites
DAMA N.V. The operator is registered in Curacao. You must
make sure that the casino can be trusted.
RocketPlay Casino Australia ensures that players can quickly access
everything they need, from games to promotions.
Whether you’re into slots, table games, or live dealers, RocketPlay Australia has something for everyone.
Rocketplay encourages all players to treat gambling as a
game, not as a financial solution.
References:
https://blackcoin.co/crown-casino-sydney-a-comprehensive-guide/
The only difference is that you can use free spins to
play the cutting-edge Bubble Bubble 2 slot with a chance of winning 50,000 times the bet per
line! The second welcome bonus on Ozwin comes with the same conditions and offers 200% of up
to $2,000 + 50 FS. If you encounter issues related to accessing the profile, you can always ask
the support care service for assistance. This completes the
registration at Ozwin Casino, you will only need
to verify your account.
Click the verification link provided in the email to activate your new account.Once
your email is verified, your Ozwin Casino account is ready to use.
They boast around 3,000 slot games, including classic
and modern video slots with engaging features.
We understand that luck can sometimes be elusive, which is why we offer a 25% – 50%
Cashback bonus to soften the blow of any losses.
References:
https://blackcoin.co/39_best-vip-online-casino-2022_rewrite_1/
Sein Pay N Play Zahlungsprinzip hat der schwedische Dienstleister sogar komplett vom deutschen Markt genommen. In diesem Fall haben wir
jedoch bessere Nachrichten für Sie, denn die Paysafecard wird mitunter sowohl von Casinos mit deutschen Lizenzen als auch von Casinos
ohne Limit akzeptiert. Das bedeutet ganz konkret, dass
Sie diese Zahlungsmethode nicht nutzen können, wenn Sie in einem Online Casino ohne Limit
spielen. Mit Inkrafttreten des neuen deutschen GlüStv änderten sich die gesetzlichen Bedingungen und PayPal kehrte wieder zurück.
Der Grund dafür ist die Lizenz, die in diesen Fällen außerhalb Deutschlands ausgestellt wurde und keine so strengen Richtlinien vorsieht, wie die deutsche Lizenz.
3fach Bonus bis 1000 € + 350 FreispieleCleobetraFastplay und
Autoplay verfügbar 100% Bonus bis 500 € + 200 FreispieleMafia CasinoSchnelle Zahlungen 100% Bonus bis 500 € + 100 FreispieleSpinplatinumkrypto-freundlicher Anbieiter 250% Bonus bis 2000 € + 250 Freispiele + 1 Bonus
CrabSpins of GloryKeine Verifizierung notwendig Wir zeigen Ihnen, welche die besten Online Casinos ohne Einzahlungslimit und Einsatzlimit auskommen.
Aber heißt das, dass auch Jugendliche im Casino spielen können? Nicht so bei Online
Casinos ohne Limit, denn dort kann man nach der Registrierung ohne Verifizierung sofort spielen. Nutzen Sie ruhig
die Gelegenheit, im Online Casino Slots mit Spielgeld spielen zu können.
References:
https://online-spielhallen.de/alles-wichtige-zur-24-casino-auszahlung/